【题目】如图所示,△ABC的外接圆⊙O的半径为2,过点C作∠ACD=∠ABC,交BA的延长线于点D,若∠ABC=45°,∠D=30°. 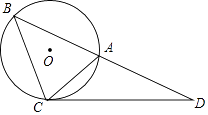
(1)求证:CD是⊙O的切线;
(2)求 ![]() 的长.
的长.
参考答案:
【答案】
(1)证明:连接OA、OC.则∠AOC=2∠ABC=90°,
∵在△AOC中,OA=OC,
∴∠OCA=∠OAC=45°,
又∵∠ACD=45°,
∴∠OCD=∠OCA+∠ACD=45°+45°=90°,
∴OC⊥CD.
即CD是⊙O的切线
(2)解:连接OB.
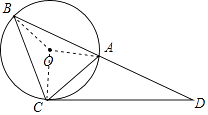
∵∠ABC=45°,∠D=30°,∠ACD=∠ABC=45°,
∴在△BCD中,∠BCD=180°﹣∠ABC﹣∠D=180°﹣45°﹣30°=105°,
∴∠ACB=∠BCD﹣∠ACD=105°﹣45°=60°,
∴∠AOB=2∠ACB=120°,
∴ ![]() 的长为:
的长为: ![]() =
= ![]() .
.
【解析】(1)证明:连接OA、OC,得到∠AOC=2∠ABC=90°,求得∠OCA=∠OAC=45°,于是得到OC⊥CD.由切线的判定定理即可得到结论;(2)连接OB.根据三角形的内角和得到∠ACB=∠BCD﹣∠ACD=105°﹣45°=60°,由圆周角定理得到∠AOB=2∠ACB=120°,根据弧长公式即可得到结论.
【考点精析】通过灵活运用三角形的外接圆与外心和切线的判定定理,掌握过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC,∠C=90°,AC≠BC.
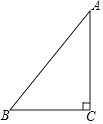
(1)请用尺规作图(不写作法,保留作图痕迹).
①作∠B的角平分线,与AC相交于点D;
②以点B为圆心、BC为半径画弧交AB于点E,连接DE.
(2)根据(1)所作的图形,写出一对全等三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生,每年的4月23日被联合国教科文组织确定为“世界读书日”某校本学年开展了读书活动,在这次活动中,八年级
 班40名学生读书册数的情况如表
班40名学生读书册数的情况如表读书册数
4
5
6
7
8
人数
 人
人
6
4
10
12
8
根据表中的数据,求:
(1)该班学生读书册数的平均数;
(2)该班学生读书册数的中位数.
-
科目: 来源: 题型:
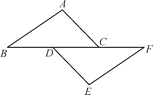
查看答案和解析>>【题目】如图,点D,C在BF上,AC∥DE,∠A=∠E,BD=CF.
(1)求证:AB=EF;
(2)连接AF,BE,猜想四边形ABEF的形状,并说明理由.
-
科目: 来源: 题型:
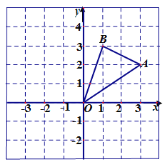
查看答案和解析>>【题目】如图,在边长为1的正方形组成的网格中,三角形AOB的顶点均在格点上,A(3,2),B(1,3),
(1)将三角形AOB先向左平移3个单位长度,后向下平移1个单位得到三角形A1O1B1,请直接作出三角形A1O1B1;
(2)请直接写出三角形A1O1B1三个顶点的坐标;
(3)三角形A1O1B1的面积为_______平方单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知购买1盆甲种花卉和3盆乙种花卉共需125元,购买3盆甲种花卉和2盆乙种花卉共需165元.
(1)求购买1盆甲种花卉和购买1盆乙种花卉各需多少元?
(2)某校为绿化校园决定购买甲乙两种花卉共60盆,要求购买的甲种花卉盆数不少于乙种花卉的 ,请帮该校设计一种最省钱的购买方案,并计算此时购买这两种花卉所需的费用.
,请帮该校设计一种最省钱的购买方案,并计算此时购买这两种花卉所需的费用.
相关试题

