【题目】已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作等边△ADE(顶点A、D、E按逆时针方向排列),连接CE.
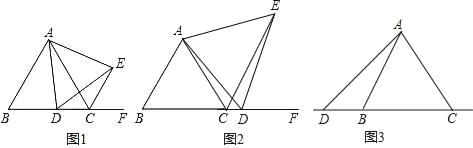
(1)如图1,当点D在边BC上时,求证:①BD=CE,②AC=CE+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CE+CD是否成立?若不成立,请写出AC、CE、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边BC的反向延长线上且其他条件不变时,补全图形,并直接写出AC、CE、CD之间存在的数量关系.
参考答案:
【答案】(1)①证明见解析;②证明见解析;(2)AC=CE+CD不成立,AC、CE、CD之间存在的数量关系是:AC=CE﹣CD,理由见解析;(3)补图见解析;AC=CD﹣CE.
【解析】
(1)根据等边三角形的性质及等式的性质证明△ABD≌△ACE,从而得出结论;
(2)根据等边三角形的性质及等式的性质就可以得出△ABD≌△ACE,就可以得出BD=CE,就可以得出AC=CE﹣CD;
(3)先根据条件画出图形,根据等边三角形的性质及等式的性质就可以得出△ABD≌△ACE,就可以得出BD=CE,就可以得出AC=CD﹣CE.
(1)∵△ABC和△ADE都是等边三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,即∠BAD=∠CAE.
在△ABD和△ACE中,
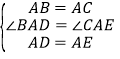 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE.
∵BC=BD+CD,AC=BC,
∴AC=CE+CD;
(2)AC=CE+CD不成立,
AC、CE、CD之间存在的数量关系是:AC=CE﹣CD.
理由:∵△ABC和△ADE都是等边三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE
在△ABD和△ACE中,
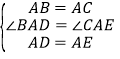
∴△ABD≌△ACE(SAS)
∴BD=CE
∴CE﹣CD=BD﹣CD=BC=AC,
∴AC=CE﹣CD;
(3)补全图形(如图)
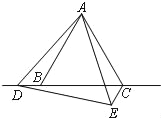
AC、CE、CD之间存在的数量关系是:AC=CD﹣CE.
理由:∵△ABC和△ADE都是等边三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°.
∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,
∴∠BAD=∠CAE
在△ABD和△ACE中,
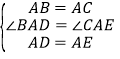
∴△ABD≌△ACE(SAS)
∴BD=CE.
∵BC=CD﹣BD,
∴BC=CD﹣CE,
∴AC=CD﹣CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究:
如图,直线
 与
与 轴,
轴, 轴分别交于
轴分别交于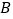 ,
,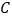 两点,其中
两点,其中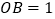 .
.
(1)求
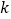 的值;
的值;(2)若点
 是直线
是直线 上的一个动点,当点
上的一个动点,当点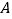 仅在第一象限内运动时,试写出
仅在第一象限内运动时,试写出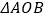 的面积
的面积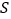 与
与 的函数关系式;
的函数关系式;(3)探索:
①在(2)条件下,当点
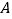 运动到什么位置时,
运动到什么位置时,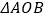 的面积是
的面积是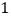 ;
;②在①成立的情况下,在
 轴上是否存在一点
轴上是否存在一点 ,使△
,使△ 是等腰三角形?若存在,请写出满足条件的所有
是等腰三角形?若存在,请写出满足条件的所有 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察图中给出的四个点阵,s表示每个点阵中的点的个数,按照图形中的点的个数变化规律,猜想第10个点阵中的点的个数s为( ).
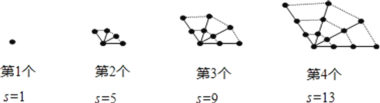
A.
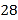 B.
B.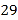 C.
C.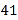 D.
D.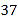
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】网络技术的发展对学生学习方式产生巨大的影响,某校为了解学生每周课余利用网络资源进行自主学习的时间,在本校随机抽取若干名学生进行问卷调查,下面是根据调查结果绘制成的不完整的统计图表:
请根据图表中的信息解答下列问题:
组别
学习时间x(h)
频数(人数)
A
0<x≤1
8
B
1<x≤2
24
C
2<x≤3
32
D
3<x≤4
n
E
4小时以上
4
(1)表中的n= ,扇形统计图中B组对应的圆心角为 °;
(2)请补全频数分布直方图;
(3)该校准备召开利用网络资源进行自主学习的交流会,计划在E组学生中随机选出两人进行经验介绍,已知E组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.

-
科目: 来源: 题型:
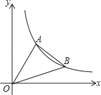
查看答案和解析>>【题目】如图,直线y=
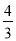 x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=
x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=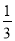 .
.(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)求S△OAB.
-
科目: 来源: 题型:
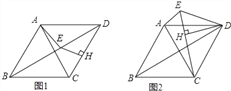
查看答案和解析>>【题目】已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)如图1,线段EH、CH、AE之间的数量关系是 ;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH.
相关试题

