【题目】综合与探究:
如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,其中
两点,其中![]() .
.

(1)求![]() 的值;
的值;
(2)若点![]() 是直线
是直线![]() 上的一个动点,当点
上的一个动点,当点![]() 仅在第一象限内运动时,试写出
仅在第一象限内运动时,试写出![]() 的面积
的面积![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)探索:
①在(2)条件下,当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积是
的面积是![]() ;
;
②在①成立的情况下,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使△
,使△![]() 是等腰三角形?若存在,请写出满足条件的所有
是等腰三角形?若存在,请写出满足条件的所有![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)k=2;(2)S=x-1;(3)①当![]() 的坐标为
的坐标为![]() 时,
时,![]() 的面积是
的面积是![]() ;②存在,点
;②存在,点![]() 坐标P1(-2
坐标P1(-2![]() ,0),P2(2
,0),P2(2![]() ,0),P3(4,0),P4(2,0)..
,0),P3(4,0),P4(2,0)..
【解析】
(1)先确定出点B的坐标,代入函数解析式中即可求出k;
(2)借助(1)得出的函数关系式,利用三角形的面积公式即可求出函数关系式;
(3)①利用三角形的面积求出求出点A坐标;
(1)∵OB=1,
∴B(1,0),
∵点B在直线y=kx-2上,
∴k-2=0,
∴k=2
(2)由(1)知,k=2,
∴直线BC解析式为y=2x-2,
∵点A(x,y)是第一象限内的直线y=2x-2上的一个动点,
∴y=2x-2(x>1),
∴S=S△AOB=![]() ×OB×|yA|=
×OB×|yA|=![]() ×1×|2x-2|=x-1,
×1×|2x-2|=x-1,
(3)①如图,
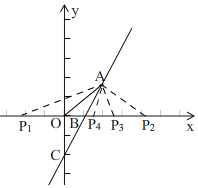
由(2)知,S=x-1,
∵△AOB的面积是1;
∴x=2,
∴A(2,2),
∴OA=2![]() ,
,
②设点P(m,0),
∵A(2,2),
∴OP=|m|,AP=![]() ,
,
①当OA=OP时,
∴2![]() =|m|,
=|m|,
∴m=±2![]() ,
,
∴P1(-2![]() ,0),P2(2
,0),P2(2![]() ,0),
,0),
②当OA=AP时,
∴2![]() =
=![]() ,
,
∴m=0或m=4,
∴P3(4,0),
③当OP=AP时,
∴|m|=![]() ,
,
∴m=2,
∴P4(2,0),
即:满足条件的所有P点的坐标为P1(-2![]() ,0),P2(2
,0),P2(2![]() ,0),P3(4,0),P4(2,0).
,0),P3(4,0),P4(2,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】附加题:(y﹣z)2+(x﹣y)2+(z﹣x)2=(y+z﹣2x)2+(z+x﹣2y)2+(x+y﹣2z)2.
求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】节约用水是我们的美德,水龙头关闭不严会造成滴水,容器内盛水
 与滴水时间
与滴水时间 的关系用可以显示水量的容器做如图
的关系用可以显示水量的容器做如图 的试验,并根据试验数据绘制出如图
的试验,并根据试验数据绘制出如图 的函数图象,结合图象解答下列问题.
的函数图象,结合图象解答下列问题.(
 )容器内原有水多少升.
)容器内原有水多少升.(
 )求
)求 与
与 之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.
之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
在学习“可化为一元一次方程的分式方程及其解法”的过程中,老师提出一个问题:若关于x的分式方程
 =1的解为正数,求a的取值范围.
=1的解为正数,求a的取值范围.经过独立思考与分析后,小杰和小哲开始交流解题思路如下:
小杰说:解这个关于x的分式方程,得x=a+4.由题意可得a+4>0,所以a>﹣4,问题解决.
小哲说:你考虑的不全面,还必须保证x≠4,即a+4≠4才行.
(1)请回答: 的说法是正确的,并简述正确的理由是 ;
(2)参考对上述问题的讨论,解决下面的问题:
若关于x的方程
 的解为非负数,求m的取值范围.
的解为非负数,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察图中给出的四个点阵,s表示每个点阵中的点的个数,按照图形中的点的个数变化规律,猜想第10个点阵中的点的个数s为( ).
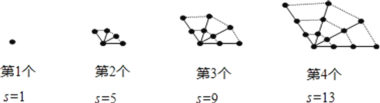
A.
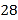 B.
B.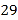 C.
C.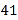 D.
D.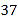
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).

-
科目: 来源: 题型:
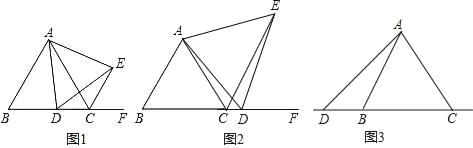
查看答案和解析>>【题目】已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作等边△ADE(顶点A、D、E按逆时针方向排列),连接CE.
(1)如图1,当点D在边BC上时,求证:①BD=CE,②AC=CE+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CE+CD是否成立?若不成立,请写出AC、CE、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边BC的反向延长线上且其他条件不变时,补全图形,并直接写出AC、CE、CD之间存在的数量关系.
相关试题

