【题目】如图,在等边△ABC中,AB=6,AD⊥BC于点D.点P在边AB上运动,过点P作PE∥BC,与边AC交于点E,连接ED,以PE、ED为邻边作平行四边形PEDF.设线段AP的长为x(0<x<6). 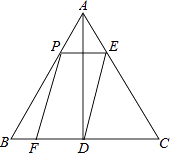
(1)求线段PE的长.(用含x的代数式表示)
(2)当四边形PEDF为菱形时,求x的值.
参考答案:
【答案】
(1)解:∵PE∥BC,
∴△APE∽△ABC,
又∵△ABC是等边三角形,
∴△APE是等边三角形,
∴PE=AP=x(0<x<6);
(2)解:∵四边形PEDF为菱形,
∴PE=DE=x,
又∵△APE是等边三角形,则AE=PE,
∴AE=DE,
∴∠DAC=∠ADE,
又∵∠ADE+∠EDC=∠DAC+∠C=90°,
∴∠EDC=∠C,
∴DE=EC,
∴DE=EC=AE= ![]() AC=
AC= ![]() AB=3,
AB=3,
即x=3.
【解析】(1)由PE与BC平行,得到三角形APE与三角形ABC相似,根据三角形ABC为等边三角形,得到三角形APE为等边三角形,可得出PE=AP=x;(2)若四边形PEDF为菱形,得到PE=DE=x,由三角形APE为等边三角形得到AE=PE,可得出AE=DE,利用等边对等角得到∠DAC=∠ADE,利用等式的性质得到∠EDC=∠C,利用等角对等边得到DE=EC,即可求出x的值;
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°,以及对菱形的性质的理解,了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y=
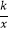 (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=
(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y= 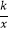 (k≠0)上的点D1处,则a= .
(k≠0)上的点D1处,则a= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算与解不等式式
(1)计算(π﹣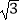 )0+(
)0+(  )﹣1﹣
)﹣1﹣ 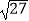
(2)解不等式组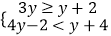 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
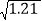 = ; (2)
= ; (2)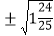 = ; (3)
= ; (3) ;
;(4)
 ; (5)
; (5)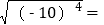 ; (6)a3·a3= ;
; (6)a3·a3= ;(7) (x3)5= ; (8)(-2x2y3)3= ; (9) (x-y)6÷(x-y)3= ;
(10)a2b(ab-4b2) (11)(2a-3b)(2a+5b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据如表回答下列问题:
x
16.2
16.3
16.4
16.5
16.6
16.7
16.8
16.9
17.0
x2
262.44
265.69
268.96
272.25
275.56
278.89
282.24
285.61
289
(1)275.56的平方根是______ ;
(2)
 = ______ ;
= ______ ;(3)查看上表, <
 < .
< . -
科目: 来源: 题型:
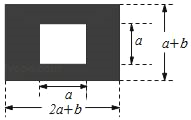
查看答案和解析>>【题目】如图,某市有一块长为(2a+b)米,宽为(a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)试用含a,b的代数式表示绿化的面积是多少平方米?
(2)若a=3,b=2,请求出绿化面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在同一直角坐标系中,一次函数y=
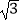 x﹣2的图象和反比例函数y=
x﹣2的图象和反比例函数y= 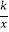 的图象的一个交点为A(
的图象的一个交点为A( 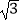 ,m).
,m).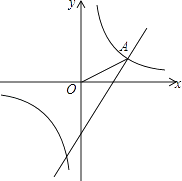
(1)求m的值及反比例函数的解析式.
(2)若点P在x轴上,且△AOP为等腰三角形,请直接写出点P的坐标.
相关试题

