【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=AB·AD,我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则∠DAB=_________.
(2)如图3,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,BC=2,∠D=90°,求AD的长?

图1 图2 图3
参考答案:
【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】试题分析:(1)、根据“可分四边形”和“可分角”的定义得出答案;(2)、根据角平分线的性质得出∠DAC=∠CAB=30°,∠DCA=150°-∠ACB,然后根据角度之间的关系得出∠ADC=∠ACB,从而说明△ACD和△ABC相似,从而得出结论;(3)、根据“可分四边形”和“可分角”的性质得出∠DAC=∠CAB, ![]() ,从而说明△ACD和△ABC相似,根据相似得出∠ACB=∠D=90°,然后根据勾股定理求出AB的长度,结合
,从而说明△ACD和△ABC相似,根据相似得出∠ACB=∠D=90°,然后根据勾股定理求出AB的长度,结合![]() 得出AD的长度.
得出AD的长度.
试题解析:(1)![]()
(2)∵AC平分∠DAB,∠DAB=60° ∴∠DAC=∠CAB=30° ∵∠DCB=150°
∴∠DCA=150°-∠ACB
在△ADC中,∠ADC=180°- ∠DAC- ∠DCA =180°-30°-(150°-∠ACB)=∠ACB
∴△ACD∽△ABC ∴![]() ∴
∴![]() , 即证四边形ABCD为“可分四边形”
, 即证四边形ABCD为“可分四边形”
(3)∵四边形ABCD为“可分四边形”,∠DAB为“可分角”∴AC平分∠DAB, ![]()
即∠DAC=∠CAB, ![]() ∴△ACD∽△ABC ∴∠ACB=∠D=90°
∴△ACD∽△ABC ∴∠ACB=∠D=90°
在Rt△ACB中AB= ![]() ∵
∵![]() ∴AD=
∴AD=![]()
-
科目: 来源: 题型:
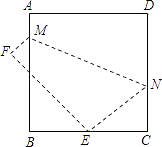
查看答案和解析>>【题目】如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN长是( )
A.3cm
B.4cm
C.5cm
D.6cm -
科目: 来源: 题型:
查看答案和解析>>【题目】为了改善居民住房条件,某市计划用未来两年的时间,将城镇居民的住房面积由现在的人均约为10m2提高到12.1m2 . 若每年的年增长率相同,则年增长率为( )
A.9%
B.10%
C.11%
D.12% -
科目: 来源: 题型:
查看答案和解析>>【题目】多项式5xy2-25x2y各项的公因式为( )
A. 5 B. 5x C. 5xy D. 25xy
-
科目: 来源: 题型:
查看答案和解析>>【题目】试确定实数a的取值范围,使不等式组
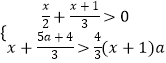 恰有两个整数解.
恰有两个整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式用提取公因式法分解因式正确的是( )
A. a2b+7ab-b=b(a2+7a)
B. 3x2y-3xy+6y=3y(x2-x+2)
C. 4x4-2x3y=x3(4x-2y)
D. -2a2+4ab-6ac=-2a(a-2b-3c)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程(组):
(1)
(2)解二元一次方程组 有位同学是这么做的,①+②得4x=20,解得x=5,代入①得y=﹣3.
有位同学是这么做的,①+②得4x=20,解得x=5,代入①得y=﹣3.
∴这个方程组的解为 .
.
该同学解这个二元一次方程组的过程中使用了消元法,目的是把二元一次方程组转化为求解;
(3)请你换一种方法来求解(2)中二元一次方程组.
相关试题

