【题目】如图,![]() 中,
中,![]() 是
是![]() 边上一点,
边上一点,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 边上的动点,且始终保持
边上的动点,且始终保持![]() .
.


(1)求![]() 的长;
的长;
(2)若四边形![]() 为平行四边形时,求
为平行四边形时,求![]() 的周长;
的周长;
(3)将![]() 沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,求线段
沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,求线段![]() 的长.
的长.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)BP=
;(3)BP=![]() 或3或
或3或![]() .
.
【解析】
(1)先根据题意推出△ABE是等腰直角三角形,再根据勾股定理计算即可.
(2)首先要推出△CPQ是等腰直角三角形,再根据已知推出各边的长度,然后相加即可.
(3)首先证明△BPE∽△CQP,然后分三种情况讨论,分别求解,即可解决问题.
(1)∵四边形ABCD是平行四边形,
∴AB=CD,
∵BE=CD=3,
∴AB=BE=3,
又∵∠A=45°,
∴∠BEA=∠A=45°,∠ABE=90°,
根据勾股定理得AE=![]() =
=![]() ;
;
(2)∵四边形ABCD是平行四边形,
∴AB=CD,∠A=∠C=45°,
又∵四边形ABPE是平行四边形,
∴BP∥AB,且AE=BP,
∴BP∥CD,
∴ED=CP=![]() ,
,
∵∠EPQ=45°,
∴∠PQC=∠EPQ=45°,
∴∠PQC=∠C=45°,∠QPC=90°,
∴CP=PQ=![]() ,QC=2,
,QC=2,
∴△CPQ的周长=2![]() +2;
+2;
(3)解:如图,作BH⊥AE于H,连接BE.

∵四边形ABCD是平行四边形,
∴AB=CD=3,AD=BC=AE+ED=![]() ,∠A=∠C=45°,
,∠A=∠C=45°,
∴AH=BH=![]() ,HE=AD-AH-DE=
,HE=AD-AH-DE=![]()
∴BH=EH,
∴∠EBH=∠HEB=∠EBC=45°,
∴∠EBP=∠C=45°,
∵∠BPQ=∠EPB+∠EPQ=∠C+∠PQC,∠EPQ=∠C,
∴∠EPB=∠PQC,
∴△BPE∽△CQP.
①当QP=QC时,则BP=PE,
∴∠EBP=∠BEP=45°,则∠BPE=90°,
∴四边形BPEF是矩形,
BP=EF=![]() ,
,
②当CP=CQ时,则BP=BE=3,
③当CP=PQ时,则BE=PE=3,∠BEP=90°,
∴△BPE为等腰三角形,
∴BP2=BE2+PE2,
∴BP=![]() ,
,
综上:BP=![]() 或3或
或3或![]() .
.
-
科目: 来源: 题型:
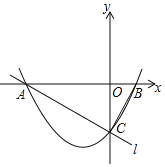
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=
 x2+
x2+ x﹣2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.
x﹣2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.(1)求直线l的解析式;
(2)若直线x=m(m<0)与该抛物线在第三象限内交于点E,与直线l交于点D,连接OD.当OD⊥AC时,求线段DE的长;
(3)取点G(0,﹣1),连接AG,在第一象限内的抛物线上,是否存在点P,使∠BAP=∠BCO﹣∠BAG?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线AC折叠,使点B翻折到点E处,若
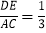 ,则
,则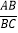 的值为( )
的值为( )
A.
 B.
B. 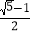 C.
C. 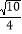 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在反比例函数y=
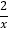 (x>0)的图象上,点B在反比例函数y=
(x>0)的图象上,点B在反比例函数y=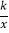 (x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积为2,则k的值为_____.
(x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积为2,则k的值为_____.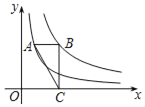
-
科目: 来源: 题型:
查看答案和解析>>【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果为“A非常了解”、“B了解”、“C基本了解”三个等级,并根据调查结果制作了如下两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
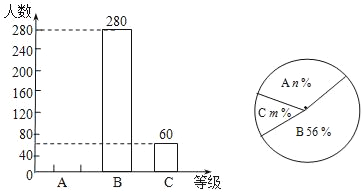
(1)本次调查的人数为 ;
(2)补全条形统计图;
(3)若该市约有市民100万人,请你根据抽样调查的结果,估计该市大约有多少人对“社会主义核心价值观”达到“A非常了解”的程度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有除颜色外其余均相同的5个小球,其中红球3个,黑球2个.
(1)若先从袋中取出x(x>0)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,若A为必然事件,则x的值为 ;
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,用画树状图或列表法求这个事件的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,测得B,C两点的俯角分别为60°和45°,已知热气球离地面的高度为120m,且大桥与地面在同一水平面上,求大桥BC的长度(结果保留整数,
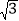 ≈1.72).
≈1.72).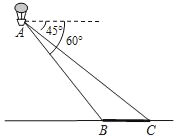
相关试题

