【题目】如图,二次函数y=![]() x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
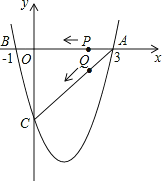
(1)求该二次函数的解析式及点C的坐标;
(2)当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E,使得以A,E,Q为顶点的三角形为等腰三角形?若存在,请求出E点坐标;若不存在,请说明理由.
(3)当P,Q运动到t秒时,△APQ沿PQ翻折,点A恰好落在抛物线上D点处,请判定此时四边形APDQ的形状,并求出D点坐标.
参考答案:
【答案】(1)C(0,-4).(2)存在.点E的坐标为(-![]() ,0)或(-
,0)或(-![]() ,0)或(-1,0)或(7,0).(3)四边形APDQ为菱形,D点坐标为(-
,0)或(-1,0)或(7,0).(3)四边形APDQ为菱形,D点坐标为(-![]() ,-
,-![]() ).
).
【解析】试题分析:(1)将A,B点坐标代入函数y=![]() x2+bx+c中,求得b、c,进而可求解析式及C坐标.
x2+bx+c中,求得b、c,进而可求解析式及C坐标.
(2)等腰三角形有三种情况,AE=EQ,AQ=EQ,AE=AQ.借助垂直平分线,画圆易得E大致位置,设边长为x,表示其他边后利用勾股定理易得E坐标.
(3)注意到P,Q运动速度相同,则△APQ运动时都为等腰三角形,又由A、D对称,则AP=DP,AQ=DQ,易得四边形四边都相等,即菱形.利用菱形对边平行且相等等性质可用t表示D点坐标,又D在E函数上,所以代入即可求t,进而D可表示.
试题解析:(1)∵二次函数y=![]() x2+bx+c的图象与x轴交于A(3,0),B(-1,0),
x2+bx+c的图象与x轴交于A(3,0),B(-1,0),
∴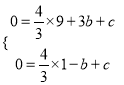 ,解得
,解得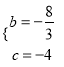 ,
,
∴y=![]() x2-
x2-![]() x-4.
x-4.
∴C(0,-4).
(2)存在.
如图1,过点Q作QD⊥OA于D,此时QD∥OC,
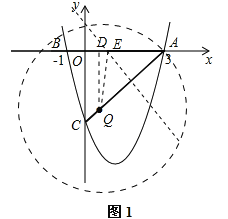
∵A(3,0),B(-1,0),C(0,-4),O(0,0),
∴AB=4,OA=3,OC=4,
∴AC=![]() =5,
=5,
∵当点P运动到B点时,点Q停止运动,AB=4,
∴AQ=4.
∵QD∥OC,
∴![]() ,
,
∴![]() ,
,
∴QD=![]() ,AD=
,AD=![]() .
.
①作AQ的垂直平分线,交AO于E,此时AE=EQ,即△AEQ为等腰三角形,
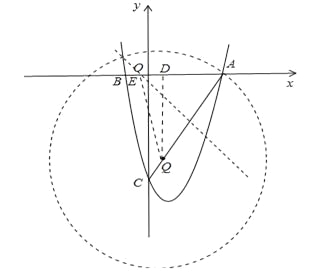
设AE=x,则EQ=x,DE=AD-AE=|![]() -x|,
-x|,
∴在Rt△EDQ中,( ![]() -x)2+(
-x)2+(![]() )2=x2,解得 x=
)2=x2,解得 x=![]() ,
,
∴OA-AE=3-![]() =-
=-![]() ,
,
∴E(-![]() ,0),
,0),
说明点E在x轴的负半轴上;
②以Q为圆心,AQ长半径画圆,交x轴于E,此时QE=QA=4,
∵ED=AD=![]() ,
,
∴AE=![]() ,
,
∴OA-AE=3-![]() =-
=-![]() ,
,
∴E(-![]() ,0).
,0).
③当AE=AQ=4时,
1.当E在A点左边时,
∵OA-AE=3-4=-1,
∴E(-1,0).
2.当E在A点右边时,
∵OA+AE=3+4=7,
∴E(7,0).
综上所述,存在满足条件的点E,点E的坐标为(-![]() ,0)或(-
,0)或(-![]() ,0)或(-1,0)或(7,0).
,0)或(-1,0)或(7,0).
(3)四边形APDQ为菱形,D点坐标为(-![]() ,-
,-![]() ).理由如下:
).理由如下:
如图2,D点关于PQ与A点对称,过点Q作,FQ⊥AP于F,
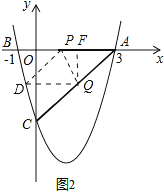
∵AP=AQ=t,AP=DP,AQ=DQ,
∴AP=AQ=QD=DP,
∴四边形AQDP为菱形,
∵FQ∥OC,
∴![]() ,
,
∴![]() ,
,
∴AF=![]() t,FQ=
t,FQ=![]() t,
t,
∴Q(3-![]() t,-
t,-![]() t),
t),
∵DQ=AP=t,
∴D(3-![]() t-t,-
t-t,-![]() t),
t),
∵D在二次函数y=![]() x2-
x2-![]() x-4上,
x-4上,
∴-![]() t=
t=![]() (3-
(3-![]() t)2-
t)2-![]() (3-
(3-![]() t)-4,
t)-4,
∴t=![]() ,或t=0(与A重合,舍去),
,或t=0(与A重合,舍去),
∴D(-![]() ,-
,-![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
 是等腰直角三角形,
是等腰直角三角形, ,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点O,求证:
,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点O,求证: .
.
-
科目: 来源: 题型:
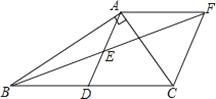
查看答案和解析>>【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=3,AB=4,求菱形ADCF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家小型放映厅盈利额y(元)与售票数x(张)之间的关系如图,保险部门规定:观众超过150人,要缴纳保险费50元,试根据图像回答问题:

(1)该放映厅有 个座位,该放映厅演出一场电影所需各项成本总和是 元;每张票的售价是 元;
(2)当售票数x为 时,不赔不赚:售票数x为 时,赔本;要获得最大利润150元,售票数x应为 张.
(3)当售票数x是多少张时,所得的利润和卖出150张时的利润相等(列方程解答)?当售票数满足什么条件时,此时利润比x=150张时多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4
 ,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,
,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,  经过点C,则图中阴影部分的面积为( )
经过点C,则图中阴影部分的面积为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2017的横坐标为( )

A. 1010 B. 2 C. 1 D. ﹣1006
-
科目: 来源: 题型:
查看答案和解析>>【题目】跃壮五金商店准备从宁云机械厂购进甲、乙两种零件进行销售.若每个甲种零件的进价比每个乙种零件的进价少2元,且用80元购进甲种零件的数量与用100元购进乙种零件的数量相同.
(1)求每个甲种零件、每个乙种零件的进价分别为多少元?
(2)若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,该五金商店每个甲种零件的销售价格为12元,每个乙种零件的销售价格为15元,则将本次购进的甲、乙两种零件全部售出后,可使销售两种零件的总利润(利润=售价-进价)超过371元,通过计算求出跃壮五金商店本次从宁云机械厂购进甲、乙两种零件有几种方案?请你设计出来.
相关试题

