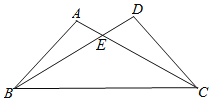
【题目】(本小题满分8分)如图,已知∠A=∠D,有下列五个条件:①AE=DE,②BE=CE,③AB=DC,④∠ABC=∠DCB,⑤AC=BD,能证明△ABC与△DCB全等的条件有几个?并选择其中一个进行证明.
参考答案:
【答案】见解析
【解析】共5个:①或②或③或④或⑤.
若选①AE=DE,则证明如下:
在△ABE和△DCE中, ,
,
∴AB=DC,BE=CE,∴DE+BE=AE+CE,∴BD=AC,
在△ABC和△DCB中, ,∴△ABC≌△DCB(SSS);(2分)
,∴△ABC≌△DCB(SSS);(2分)
若选②BE=CE,则证明如下:
∵BE=CE,∴∠EBC=∠ECB,
在△ABC与△DCB中, ,∴△ABC≌△DCB(AAS);(3分)
,∴△ABC≌△DCB(AAS);(3分)
若选③AB=DC,则证明如下:
在△ABE和△DCE中, ,∴△ABE≌△DCE(AAS),
,∴△ABE≌△DCE(AAS),
∴BE=CE,∴∠EBC=∠ECB,
在△ABC与△DCB中, ,∴△ABC≌△DCB(AAS);(5分)
,∴△ABC≌△DCB(AAS);(5分)
若选④∠ABC=∠DCB,则证明如下:
在△ABC与△DCB中, ,∴△ABC≌△DCB(AAS);(6分)
,∴△ABC≌△DCB(AAS);(6分)
若选⑤AC=BD,则证明如下:
如图,延长BA,CD交于点F,

∵∠BAC=∠CDB,∴∠FAC=∠FDB,
又∵∠F=∠F,BD=CA,∴△BDF≌△CAF,
∴BF=CF,AF=DF,∴AB=CD,
在△ABE和△DCE中, ,
,
∴△ABE≌△DCE(AAS),
∴BE=CE,∴∠EBC=∠ECB,
在△ABC与△DCB中, ,
,
∴△ABC≌△DCB(AAS).
综上所述,能证明△ABC与△DCB全等的条件有5个.(8分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )
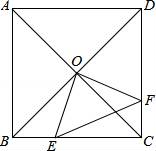
A.
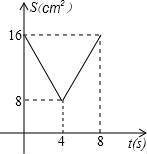
B.
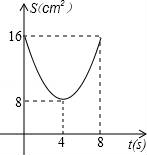
C.
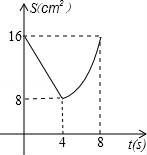
D.
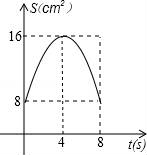
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知单项式xay3与﹣4xy4﹣b是同类项,那么a﹣b的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:OA⊥OC,∠AOB:∠AOC=2:3,画出图形,并求∠BOC的度数.
-
科目: 来源: 题型:
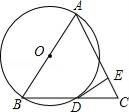
查看答案和解析>>【题目】如图,△ABC 中,AB=AC,以AB为直径作⊙O,与BC交于点D,过D作AC的垂线,垂足为E.
证明:(1)BD=DC;(2)DE是⊙O切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的直径,CD是圆O的一条弦,且CD⊥AB于点E.
(1)若∠A=48°,求∠OCE的度数;
(2)若CD=4
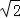 ,AE=2,求圆O的半径.
,AE=2,求圆O的半径.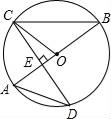
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=4,BC=3,AB=5,射线AX垂直于AC,点A为垂足,一条长度为5的线段PQ的两个端点P、Q分别在边AC和射线AX上运动,则当AP=___________ 时,ΔABC与ΔPQA全等.

相关试题

