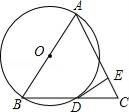
【题目】如图,△ABC 中,AB=AC,以AB为直径作⊙O,与BC交于点D,过D作AC的垂线,垂足为E.
证明:(1)BD=DC;(2)DE是⊙O切线.
参考答案:
【答案】详见解析
【解析】
试题分析:(1)连接AD,由于AB是直径,那么∠ADB=90°,而AB=AC,根据等腰三角形三线合一定理可知BD=CD;
(2)连接OD,由于∠BAC=2∠BAD,∠BOD=2∠BAD,那么∠BAC=∠BOD,可得OD∥AC,而DE⊥AC,易证∠ODB=90°,从而可证DE是⊙O切线.
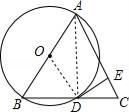
试题解析:如右图所示,
(1)连接AD,∵AB是直径,∴∠ADB=90°,又∵AB=AC,∴BD=CD;
(2)连接OD,∵∠BAC=2∠BAD,∠BOD=2∠BAD,∴∠BAC=∠BOD,∴OD∥AC,
又∵DE⊥AC,∴∠AED=90°,∴∠ODB=∠AED=90°,∴DE是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知单项式xay3与﹣4xy4﹣b是同类项,那么a﹣b的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:OA⊥OC,∠AOB:∠AOC=2:3,画出图形,并求∠BOC的度数.
-
科目: 来源: 题型:
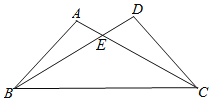
查看答案和解析>>【题目】(本小题满分8分)如图,已知∠A=∠D,有下列五个条件:①AE=DE,②BE=CE,③AB=DC,④∠ABC=∠DCB,⑤AC=BD,能证明△ABC与△DCB全等的条件有几个?并选择其中一个进行证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的直径,CD是圆O的一条弦,且CD⊥AB于点E.
(1)若∠A=48°,求∠OCE的度数;
(2)若CD=4
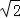 ,AE=2,求圆O的半径.
,AE=2,求圆O的半径.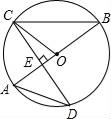
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=4,BC=3,AB=5,射线AX垂直于AC,点A为垂足,一条长度为5的线段PQ的两个端点P、Q分别在边AC和射线AX上运动,则当AP=___________ 时,ΔABC与ΔPQA全等.

-
科目: 来源: 题型:
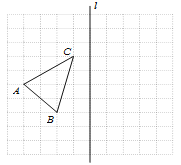
查看答案和解析>>【题目】如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)在(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.
相关试题

