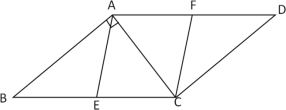
【题目】如图,已知点![]() ,
,![]() 分别是平行四边形
分别是平行四边形![]() 的边
的边![]() ,
,![]() 上的中点,且∠
上的中点,且∠![]() =90°.
=90°.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() =4,
=4,![]() =5,求菱形
=5,求菱形![]() 的面积.
的面积.
参考答案:
【答案】(1)见解析;(2)10.
【解析】
(1)由平行四边形的性质可得BC=AD,BC∥AD,由中点的性质可得EC=AF,可证四边形AECF为平行四边形,由直角三角形的性质可得AE=EC,即可得结论;
(2)可求S△ABC=![]() AB×AC=10,即可求菱形AECF的面积.
AB×AC=10,即可求菱形AECF的面积.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的中点
上的中点
∴AF∥EC ,AF=EC
∴四边形AECF是平行四边形.
在Rt△ABC中,∠BAC=90°,点E是BC边的中点,
∴AE =![]() BC=CE
BC=CE
∴平行四边形AECF是菱形.
(2)∵∠BAC=90°,AB=5,AC=4,
∴S△ABC=![]() AB×AC=10
AB×AC=10
∵点E是BC的中点,
∴S△AEC=![]() S△ABC=5
S△ABC=5
∵四边形AECF是菱形
∴四边形AECF的面积=2S△AEC=10.
-
科目: 来源: 题型:
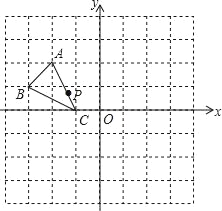
查看答案和解析>>【题目】如图,在8×8的方格中建立平面直角坐标系,有点A(﹣2,2)、B(﹣3,1)、C(﹣1,0),P(a,b)是△ABC的AC边上点,将△ABC平移后得到△A1B1C1,点P的对应点为P1(a+4,b+2).
(1)画出平移后的△A1B1C1,写出点A1、C1的坐标;
(2)若以A、B、C、D为顶点的四边形为平行四边形,写出方格中D点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】附加题:(y﹣z)2+(x﹣y)2+(z﹣x)2=(y+z﹣2x)2+(z+x﹣2y)2+(x+y﹣2z)2.
求
 的值.
的值. -
科目: 来源: 题型:
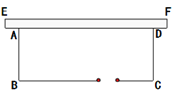
查看答案和解析>>【题目】老王想靠着一面旧墙EF,开垦一块长方形的菜地ABCD,如图所示,菜地的一边靠墙,另外三边用竹篱笆围起来,并在平行于墙的一边BC上留1米宽装门,已知现有竹篱笆长共32米,全部用完.(损耗不计)
(1)设垂直于墙面的一边AB长为x米,请用含有x的代数式来表示菜园的面积.
(2)当x=8时,求菜地面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了满足市场需求,某厂家生产A、B两种款式的环保购物袋,每天共生产5000个,两种购物袋的成本和售价如下表:
成本(元/个)
售价 (元/个)
2
2.4
3
3.6
设每天生产A种购物袋x个,每天共获利y元.
(1)求y与x的函数解析式;
(2)如果该厂每天最多投入成本12000元,那么每天最多获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
为参加学校运动会,七年级一班和七年级二班准备购买运动服. 下面是某服装厂给出的运动服价格表:
购买服装数(套)
1~35
36~60
61及61以上
每套服装价(元)
60
50
40
已知两班共有学生67人(每班学生人数都不超过60人),如果两班单独购买服装,每人只买一套,那么一共应付3650元. 问七年级一班和七年级二班各有学生多少人?
-
科目: 来源: 题型:
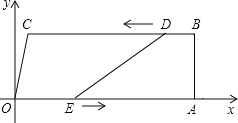
查看答案和解析>>【题目】如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.
(1)当t为何值时,四边形ABDE是矩形;
(2)当t为何值时,DE=CO?
(3)连接AD,记△ADE的面积为S,求S与t的函数关系式.
相关试题

