搜索
【题目】在棋盘中建立如图的直角坐标系，三颗棋子A，O，B的位置如图，它们分别是（﹣1，1），（0，0）和（1，0）． 
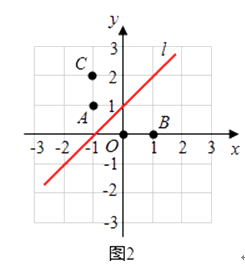
（1）如图2，添加棋子C，使A，O，B，C四颗棋子成为一个轴对称图形，请在图中画出该图形的对称轴；
（2）在其他格点位置添加一颗棋子P，使A，O，B，P四颗棋子成为一个轴对称图形，请直接写出棋子P的位置的坐标．（写出2个即可）
参考答案：
【答案】
（1）解：如图2所示，C点的位置为（﹣1，2），A，O，B，C四颗棋子组成等腰梯形，直线l为该图形的对称轴
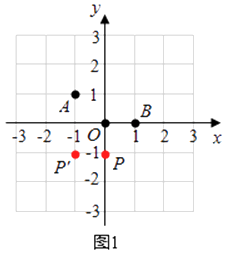
（2）解：如图1所示：P（0，﹣1），P′（﹣1，﹣1）都符合题意
【解析】（1）根据A，B，O，C的位置，结合轴对称图形的性质进而画出对称轴即可；（2）利用轴对称图形的性质得出P点位置．
-
科目： 来源： 题型：
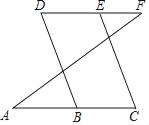
查看答案和解析>>【题目】填写理由：如图所示
∵DF∥AC（已知），
∴∠D+∠DBC=180°．（ ）
∵∠C=∠D（已知），
∴∠C+ =180°．（ ）
∴DB∥EC（ ）
∴∠D=∠CEF．（ ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在□ABCD中，E是AD的中点，延长CB到点F，使
，连接BE、AF．（1）完成画图并证明四边形AFBE是平行四边形；
（2）若AB=6，AD=8，∠C=60°，求BE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】学校计划从某苗木基地购进A、B两咱树苗共200棵绿化校园。已知购买了3棵A种树苗和5棵B种树苗共需700元；购买2棵A种树苗和1棵B种树苗共需280元．
（1）每棵A种树苗、B种树苗各需多少元？
（2）学校除支付购买树苗的费用外，平均每棵树苗还需支付运输及种植费用20元。设学校购买B种树苗x棵，购买两种树苗及运输、种植所需的总费用为y元，求y与x的函数关系；
（3）在（2）的条件下，若学校用于绿化的总费用在22400元限额内，且购买A种树苗的数量不少于B种树苗的数量，请给出一种费用最省的方案，并求出该方案所需的费用．
-
科目： 来源： 题型：
查看答案和解析>>【题目】九（3）班为了组队参加学校举行的“五水共治”知识竞赛，在班里选取了若干名学生，分成人数相同的甲、乙两组，进行了四次“五水共治”模拟竞赛，成绩优秀的人数和优秀率分别绘制成如图统计图．
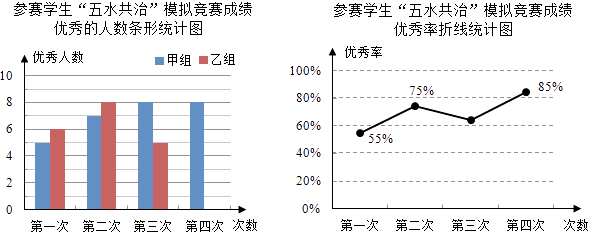
根据统计图，解答下列问题：
（1）第三次成绩的优秀率是多少？并将条形统计图补充完整；
（2）已求得甲组成绩优秀人数的平均数
=7，方差 
=1.5，请通过计算说明，哪一组成绩优秀的人数较稳定？ -
科目： 来源： 题型：
查看答案和解析>>【题目】受国内外复杂多变的经济环境影响，去年1至7月，原材料价格一路攀升，义乌市某服装厂每件衣服原材料的成本y1（元）与月份x（1≤x≤7，且x为整数）之间的函数关系如下表：
月份x
1
2
3
4
5
6
7
成本（元/件）
56
58
60
62
64
66
68
8至12月，随着经济环境的好转，原材料价格的涨势趋缓，每件原材料成本y2（元）与月份x的函数关系式为y2=x+62（8≤x≤12，且x为整数）．
（1）请观察表格中的数据，用学过的函数相关知识求y1与x的函数关系式．
（2）若去年该衣服每件的出厂价为100元，生产每件衣服的其他成本为8元，该衣服在1至7月的销售量p1（万件）与月份x满足关系式p1=0.1x+1.1（1≤x≤7，且x为整数）； 8至12月的销售量p2（万件）与月份x满足关系式p2=﹣0.1x+3（8≤x≤12，且x为整数），该厂去年哪个月利润最大？并求出最大利润． -
科目： 来源： 题型：
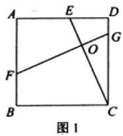
查看答案和解析>>【题目】如图1，在正方形ABCD中，点E为AD上一点，FG⊥CE分别交AB、CD于F、G，垂足为O．
（1）求证：CE=FG；
（2）如图2，连接OB，若AD=3DE，∠OBC=2∠DCE。
求
的值；若AD=3，则OE的长为_________（直接写出结果）．
相关试题
