搜索
【题目】如图，在□ABCD中，E是AD的中点，延长CB到点F，使
，连接BE、AF．
（1）完成画图并证明四边形AFBE是平行四边形；
（2）若AB=6，AD=8，∠C=60°，求BE的长．
参考答案：
【答案】（1）见解析；（2）
【解析】（1）画图，由AE∥BF，AE=BF，可证四边形AFBE是平行四边形；（2）过点A作AG⊥BF于G ,先求BG,FG,AG，再结合勾股定理求AF，得BE＝AF.
图如下，（1）∵四边形ABCD为平行四边形，
∴AD∥BC，AD=BC，
又E是AD的中点，
，
∴AE∥BF，AE=BF，
∴四边形AFBE是平行四边形；
（2）过点A作AG⊥BF于G ,
由□ABCD可知∠ABF=∠C=60°，
又AB=6，AD=8，
∴BG＝3，FG＝1，AG＝
，
∴BE＝AF＝
.
故答案为：(1)见解析；（2）.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某同学上学期的数学历次测验成绩如下表所示：
测验类别
平时测验
期中测验
期末测验
第1次
第2次
第3次
成绩
100
106
106
105
110
（1）该同学上学期5次测验成绩的众数为 ，中位数为 ；
（2）该同学上学期数学平时成绩的平均数为 ；
（3）该同学上学期的总成绩是将平时测验的平均成绩、期中测验成绩、期末测验成绩按照2：3：5的比例计算所得，求该同学上学期数学学科的总评成绩（结果保留整数）。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线MN∥PQ，点A在直线MN与PQ之间，点B在直线MN上，连结AB．∠ABM的平分线BC交PQ于点C，连结AC，过点A作AD⊥PQ交PQ于点D，作AF⊥AB交PQ于点F，AE平分∠DAF交PQ于点E，若∠CAE=45°，∠ACB=
∠DAE，则∠ACD的度数是_____．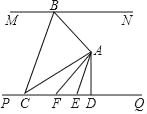
-
科目： 来源： 题型：
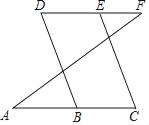
查看答案和解析>>【题目】填写理由：如图所示
∵DF∥AC（已知），
∴∠D+∠DBC=180°．（ ）
∵∠C=∠D（已知），
∴∠C+ =180°．（ ）
∴DB∥EC（ ）
∴∠D=∠CEF．（ ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】学校计划从某苗木基地购进A、B两咱树苗共200棵绿化校园。已知购买了3棵A种树苗和5棵B种树苗共需700元；购买2棵A种树苗和1棵B种树苗共需280元．
（1）每棵A种树苗、B种树苗各需多少元？
（2）学校除支付购买树苗的费用外，平均每棵树苗还需支付运输及种植费用20元。设学校购买B种树苗x棵，购买两种树苗及运输、种植所需的总费用为y元，求y与x的函数关系；
（3）在（2）的条件下，若学校用于绿化的总费用在22400元限额内，且购买A种树苗的数量不少于B种树苗的数量，请给出一种费用最省的方案，并求出该方案所需的费用．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在棋盘中建立如图的直角坐标系，三颗棋子A，O，B的位置如图，它们分别是（﹣1，1），（0，0）和（1，0）．
（1）如图2，添加棋子C，使A，O，B，C四颗棋子成为一个轴对称图形，请在图中画出该图形的对称轴；
（2）在其他格点位置添加一颗棋子P，使A，O，B，P四颗棋子成为一个轴对称图形，请直接写出棋子P的位置的坐标．（写出2个即可） -
科目： 来源： 题型：
查看答案和解析>>【题目】九（3）班为了组队参加学校举行的“五水共治”知识竞赛，在班里选取了若干名学生，分成人数相同的甲、乙两组，进行了四次“五水共治”模拟竞赛，成绩优秀的人数和优秀率分别绘制成如图统计图．
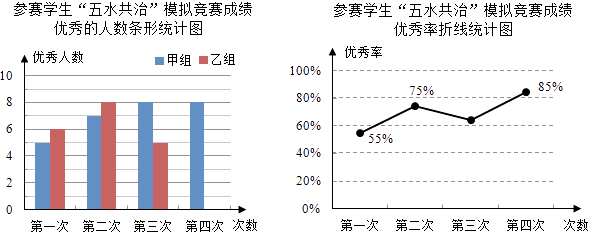
根据统计图，解答下列问题：
（1）第三次成绩的优秀率是多少？并将条形统计图补充完整；
（2）已求得甲组成绩优秀人数的平均数
=7，方差 
=1.5，请通过计算说明，哪一组成绩优秀的人数较稳定？
相关试题
