【题目】受国内外复杂多变的经济环境影响,去年1至7月,原材料价格一路攀升,义乌市某服装厂每件衣服原材料的成本y1(元)与月份x(1≤x≤7,且x为整数)之间的函数关系如下表:
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
成本(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
8至12月,随着经济环境的好转,原材料价格的涨势趋缓,每件原材料成本y2(元)与月份x的函数关系式为y2=x+62(8≤x≤12,且x为整数).
(1)请观察表格中的数据,用学过的函数相关知识求y1与x的函数关系式.
(2)若去年该衣服每件的出厂价为100元,生产每件衣服的其他成本为8元,该衣服在1至7月的销售量p1(万件)与月份x满足关系式p1=0.1x+1.1(1≤x≤7,且x为整数); 8至12月的销售量p2(万件)与月份x满足关系式p2=﹣0.1x+3(8≤x≤12,且x为整数),该厂去年哪个月利润最大?并求出最大利润.
参考答案:
【答案】
(1)解:由表格中数据可猜测,y1是x的一次函数.
设y1=kx+b
则 ![]() 解得:
解得: ![]()
∴y1=2x+54,
经检验其它各点都符合该解析式,
∴y1=2x+54(1≤x≤7,且x为整数)
(2)解:设去年第x月的利润为w万元.
当1≤x≤7,且x为整数时,
w=p1(100﹣8﹣y1)=(0.1x+1.1)(92﹣2x﹣54)=﹣0.2x2+1.6x+41.8=﹣0.2(x﹣4)2+45,
∴当x=4时,w最大=45万元;
当8≤x≤12,且x为整数时,
w=p2(100﹣8﹣y2)=(﹣0.1x+3)(92﹣x﹣62)=0.1x2﹣6x+90=0.1(x﹣30)2,
∴当x=8时,w最大=48.4万元.
∴该厂去年8月利润最大,最大利润为48.4万元
【解析】(1)由表格中数据可猜测,y1是x的一次函数.把表格(1)中任意两组数据代入直线解析式可得y1的解析式.(2)分情况探讨得:1≤x≤7时,利润=p1×(售价﹣各种成本);80≤x≤12时,利润=p2×(售价﹣各种成本);并求得相应的最大利润即.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划从某苗木基地购进A、B两咱树苗共200棵绿化校园。已知购买了3棵A种树苗和5棵B种树苗共需700元;购买2棵A种树苗和1棵B种树苗共需280元.
(1)每棵A种树苗、B种树苗各需多少元?
(2)学校除支付购买树苗的费用外,平均每棵树苗还需支付运输及种植费用20元。设学校购买B种树苗x棵,购买两种树苗及运输、种植所需的总费用为y元,求y与x的函数关系;
(3)在(2)的条件下,若学校用于绿化的总费用在22400元限额内,且购买A种树苗的数量不少于B种树苗的数量,请给出一种费用最省的方案,并求出该方案所需的费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在棋盘中建立如图的直角坐标系,三颗棋子A,O,B的位置如图,它们分别是(﹣1,1),(0,0)和(1,0).

(1)如图2,添加棋子C,使A,O,B,C四颗棋子成为一个轴对称图形,请在图中画出该图形的对称轴;
(2)在其他格点位置添加一颗棋子P,使A,O,B,P四颗棋子成为一个轴对称图形,请直接写出棋子P的位置的坐标.(写出2个即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】九(3)班为了组队参加学校举行的“五水共治”知识竞赛,在班里选取了若干名学生,分成人数相同的甲、乙两组,进行了四次“五水共治”模拟竞赛,成绩优秀的人数和优秀率分别绘制成如图统计图.
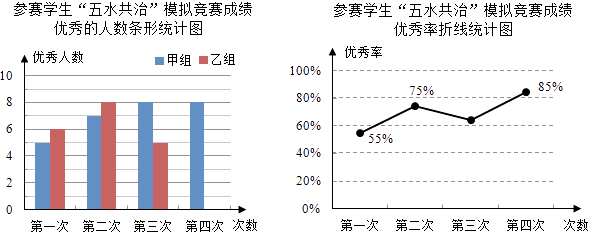
根据统计图,解答下列问题:
(1)第三次成绩的优秀率是多少?并将条形统计图补充完整;
(2)已求得甲组成绩优秀人数的平均数 =7,方差
=7,方差  =1.5,请通过计算说明,哪一组成绩优秀的人数较稳定?
=1.5,请通过计算说明,哪一组成绩优秀的人数较稳定? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为O.
(1)求证:CE=FG;
(2)如图2,连接OB,若AD=3DE,∠OBC=2∠DCE。
求
 的值;
的值;若AD=3,则OE的长为_________(直接写出结果).
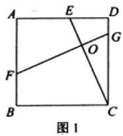

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1经过过点P(2,2),分别交x轴、y轴于点A(4,0),B。
(1)求直线l1的解析式;
(2)点C为x轴负半轴上一点,过点C的直线l2:
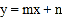 交线段AB于点D。
交线段AB于点D。如图1,当点D恰与点P重合时,点Q(t,0)为x轴上一动点,过点Q作QM⊥x轴,分别交直线l1、l2于点M、N。若
 ,MN=2MQ,求t的值;
,MN=2MQ,求t的值;如图2,若BC=CD,试判断m,n之间的数量关系并说明理由。
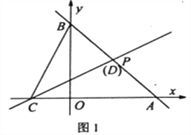
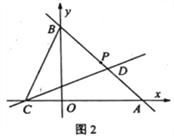
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=
 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=  ,OB=4,OE=2.
,OB=4,OE=2. 
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO , 求点D的坐标.
相关试题

