【题目】如图,山脚下有一棵树AB,小强从点B沿山坡向上走50m到达点D,用高为1.5m的测角仪CD测得树顶为10°,已知山坡的坡脚为15°,则树AB的高=(精确到0.1m)(已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin15°≈0.26,cos15°≈0.97,tan15°≈0.27).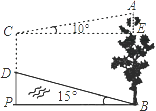
参考答案:
【答案】23.2m
【解析】解:由题意可得,
BD=50m,CD=1.5m,∠ACE=10°,∠DBP=15°,
∴DP=BDsin15°≈50×0.26=13m,
BP=BDcos15°≈50×0.97=48.5m,
∵CE=BP,
∴AE=CEtan10°≈48.5×0.18=8.73m,
∴AB=AE+CD+DP=8.73+1.5+13=23.23≈23.2m.
所以答案是:23.2m.
【考点精析】本题主要考查了关于坡度坡角问题的相关知识点,需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车同时从
 地出发前往
地出发前往 地.甲车中途因故停车一段时间,之后以原速继续行驶,与乙车同时到达
地.甲车中途因故停车一段时间,之后以原速继续行驶,与乙车同时到达 地.下图是甲、乙两车离开
地.下图是甲、乙两车离开 地的路程
地的路程 与时间
与时间 之间的函数图象.
之间的函数图象.
(1)甲车每小时行驶_________千米,
 的值为________.
的值为________.(2)求甲车再次行驶过程中
 与
与 之间的函数关系式.
之间的函数关系式.(3)甲、乙两车离开
 地的路程差为8千米时,直接写出
地的路程差为8千米时,直接写出 的值.
的值. -
科目: 来源: 题型:
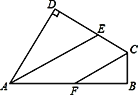
查看答案和解析>>【题目】已知:如图所示,四边形ABCD中,∠B=∠D=90°,AE平分∠DAB,AE//CF.
(1)说明:CF平分∠BCD;
(2)作△ADE的高DM,若AD=8,DE=6,AE=10,求DM的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点A在射线CE上,∠C=∠D.
⑴如图1,若AD∥BC,求证:BD∥AC;
⑵如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
⑶如图3,在⑵的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把平面内一条数轴
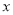 绕原点
绕原点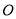 逆时针旋转角
逆时针旋转角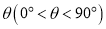 得到另一条数轴
得到另一条数轴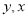 轴和
轴和 轴构成一个平面斜坐标系.过点
轴构成一个平面斜坐标系.过点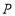 作
作 轴的平行线,交
轴的平行线,交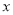 轴于点
轴于点 ,过点
,过点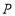 作
作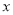 轴的平行线,交
轴的平行线,交 轴于点
轴于点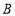 .若点
.若点 在
在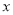 轴上对应的实数为
轴上对应的实数为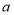 ,点
,点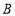 在
在 轴上对应的实数为
轴上对应的实数为 ,则成有序实数对
,则成有序实数对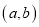 为点
为点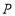 的斜坐标.
的斜坐标.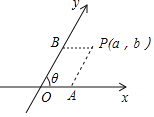
(1)在某平面斜坐标系中,已知
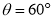 ,点
,点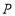 的斜坐标为
的斜坐标为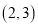 ,点
,点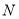 与点
与点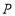 关于
关于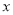 轴对称,求点
轴对称,求点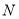 的斜坐标.
的斜坐标.(2)某平面斜坐标系中,已知点
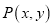 ,求出点
,求出点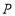 关于
关于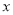 轴、
轴、 轴的对称点
轴的对称点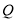 点、
点、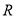 点的斜坐标.(用含
点的斜坐标.(用含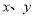 及
及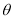 的式子表示).
的式子表示).(3)直接写出点
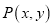 关于原点对称的点的斜坐标是_________.
关于原点对称的点的斜坐标是_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形
 的边
的边 的边分别在
的边分别在 轴,
轴, 轴正半轴上,
轴正半轴上, , 点
, 点 从点
从点 出发以每秒2个单位长度的速度向终点
出发以每秒2个单位长度的速度向终点 运动,点
运动,点 不与点
不与点 重合以
重合以 为边在
为边在 上方作正方形
上方作正方形 ,设正方形
,设正方形 与
与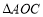 的重叠部分图形的面积为
的重叠部分图形的面积为 (平方单位),点
(平方单位),点 的运动时间为
的运动时间为 (秒).
(秒).
(1)直线
 所在直线的解析式是__________________________.
所在直线的解析式是__________________________.(2)当点
 落在线段
落在线段 上时,求
上时,求 的值.
的值.(3)在点
 运动的过程中,求
运动的过程中,求 与
与 之间的函数关系式;
之间的函数关系式;(4)设边
 的中点为
的中点为 ,点
,点 关于点
关于点 的对称点为
的对称点为 ,以
,以 为边在
为边在 上方作正方形
上方作正方形 当正方形
当正方形 与
与 重叠部分图形为三角形时,直接写出
重叠部分图形为三角形时,直接写出 的取值范围.
的取值范围.(提示:根据点
 的运动,可在草纸上画出正方形
的运动,可在草纸上画出正方形 与
与 重叠部分图形为不同图形时的临界状态去研究.)
重叠部分图形为不同图形时的临界状态去研究.) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某小区的一个健身器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
相关试题

