【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

参考答案:
【答案】(1)(m,2m﹣5);(2)S△ABC =﹣![]() ;(3)m的值为
;(3)m的值为![]() 或10+2
或10+2![]() .
.
【解析】(1)利用配方法将二次函数解析式由一般式变形为顶点式,此题得解;
(2)过点C作直线AB的垂线,交线段AB的延长线于点D,由AB∥x轴且AB=4,可得出点B的坐标为(m+2,4a+2m5),设BD=t,则点C的坐标为(m+2+t,4a+2m5t),利用二次函数图象上点的坐标特征可得出关于t的一元二次方程,解之取其正值即可得出t值,再利用三角形的面积公式即可得出S△ABC的值;
(3)由(2)的结论结合S△ABC=2可求出a值,分三种情况考虑:①当m>2m2,即m<2时,x=2m2时y取最大值,利用二次函数图象上点的坐标特征可得出关于m的一元二次方程,解之可求出m的值;②当2m5≤m≤2m2,即2≤m≤5时,x=m时y取最大值,利用二次函数图象上点的坐标特征可得出关于m的一元一次方程,解之可求出m的值;③当m<2m5,即m>5时,x=2m5时y取最大值,利用二次函数图象上点的坐标特征可得出关于m的一元一次方程,解之可求出m的值.综上即可得出结论.
(1)∵y=ax2﹣2amx+am2+2m﹣5=a(x﹣m)2+2m﹣5,
∴抛物线的顶点坐标为(m,2m﹣5),
故答案为:(m,2m﹣5);
(2)过点C作直线AB的垂线,交线段AB的延长线于点D,如图所示,
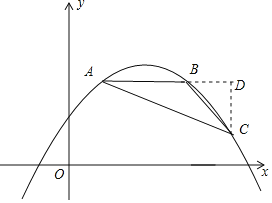
∵AB∥x轴,且AB=4,
∴点B的坐标为(m+2,4a+2m﹣5),
∵∠ABC=135°,
∴设BD=t,则CD=t,
∴点C的坐标为(m+2+t,4a+2m﹣5﹣t),
∵点C在抛物线y=a(x﹣m)2+2m﹣5上,
∴4a+2m﹣5﹣t=a(2+t)2+2m﹣5,
整理,得:at2+(4a+1)t=0,
解得:t1=0(舍去),t2=﹣![]() ,
,
∴S△ABC=![]() ABCD=﹣
ABCD=﹣![]() ;
;
(3)∵△ABC的面积为2,
∴﹣![]() =2,
=2,
解得:a=﹣![]() ,
,
∴抛物线的解析式为y=﹣![]() (x﹣m)2+2m﹣5.
(x﹣m)2+2m﹣5.
分三种情况考虑:
①当m>2m﹣2,即m<2时,有﹣![]() (2m﹣2﹣m)2+2m﹣5=2,
(2m﹣2﹣m)2+2m﹣5=2,
整理,得:m2﹣14m+39=0,
解得:m1=7﹣![]() (舍去),m2=7+
(舍去),m2=7+![]() (舍去);
(舍去);
②当2m﹣5≤m≤2m﹣2,即2≤m≤5时,有2m﹣5=2,解得:m=![]() ;
;
③当m<2m﹣5,即m>5时,有﹣![]() (2m﹣5﹣m)2+2m﹣5=2,
(2m﹣5﹣m)2+2m﹣5=2,
整理,得:m2﹣20m+60=0,
综上所述:m的值为![]() 或10+2
或10+2![]() .
.
-
科目: 来源: 题型:
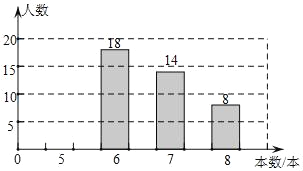
查看答案和解析>>【题目】中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书“,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本书最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表,如图所示:
本数(本)
频数(人数)
频率
5
a
0.2
6
18
0.36
7
14
b
8
8
0.16
合计
50
c
我们定义频率=
 ,比如由表中我们可以知道在这次随机调查中抽样人数为50人课外阅读量为6本的同学为18人,因此这个人数对应的频率就是
,比如由表中我们可以知道在这次随机调查中抽样人数为50人课外阅读量为6本的同学为18人,因此这个人数对应的频率就是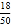 =0.36.
=0.36.(1)统计表中的a、b、c的值;
(2)请将频数分布表直方图补充完整;
(3)求所有被调查学生课外阅读的平均本数;
(4)若该校八年级共有600名学生,你认为根据以上调查结果可以估算分析该校八年级学生课外阅读量为7本和8本的总人数为多少吗?请写出你的计算过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲是一个大长方形剪去一个小长方形后形成的图形,已知动点P以每秒2cm的速度沿图甲的边框按从B→C→D→E→F→A的路径移动,相应的△ABP的面积S与时间t之间的关系如图乙中的图象表示.若AB=6cm,试回答下列问题
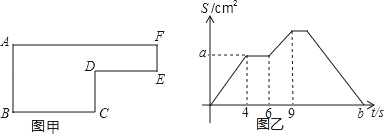
(1)图甲中的BC长是多少?
(2)图乙中的a是多少?
(3)图甲中的图形面积的多少?
(4)图乙中的b是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为
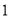 的正方形
的正方形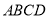 绕点
绕点 逆时针旋转
逆时针旋转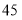 度后得到正方形
度后得到正方形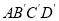 ,边
,边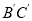 与
与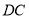 交于点
交于点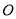 ,则四边形
,则四边形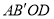 的周长是_______________.
的周长是_______________.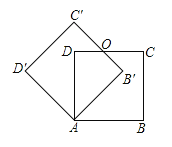
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式
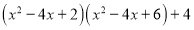 进行因式分解的过程.
进行因式分解的过程.解:设
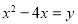 ,
,原式
 (第一步)
(第一步)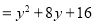 (第二步)
(第二步)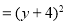 (第三步)
(第三步)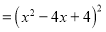 (第四步)
(第四步)回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_____________.
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底__________(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设
 =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;(3)当∠ABE的正切值是
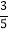 时,求AB的长.
时,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】P是⊙O内一点,过点P作⊙O的任意一条弦AB,我们把PAPB的值称为点P关于⊙O的“幂值”
(1)⊙O的半径为6,OP=4.
①如图1,若点P恰为弦AB的中点,则点P关于⊙O的“幂值”为_____;
②判断当弦AB的位置改变时,点P关于⊙O的“幂值”是否为定值,若是定值,证明你的结论;若不是定值,求点P关于⊙0的“幂值”的取值范围;
(2)若⊙O的半径为r,OP=d,请参考(1)的思路,用含r、d的式子表示点P关于⊙O的“幂值”或“幂值”的取值范围_____;
(3)在平面直角坐标系xOy中,C(1,0),⊙C的半径为3,若在直线y=
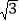 x+b上存在点P,使得点P关于⊙C的“幂值”为6,请直接写出b的取值范围_____.
x+b上存在点P,使得点P关于⊙C的“幂值”为6,请直接写出b的取值范围_____.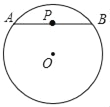
相关试题

