【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为_____________.

参考答案:
【答案】120°
【解析】作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值。作DA延长线AH,
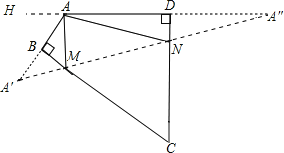
∵∠DAB=120°,
∴∠HAA′=60°,
∴∠AA′M+∠A″=∠HAA′=60°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A'=2(∠AA′M+∠A')=2×60°=120°。
故答案为:120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.
以上结论正确的有( )个.
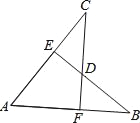
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校5月份举行了八年级生物实验考查,有A和B两个考查实验,规定每位学生只参加其中一个实验的考查,并由学生自己抽签决定具体的考查实验,小明、小丽、小华都参加了本次考查.
(1)小丽参加实验A考查的概率是 ;
(2)用列表或画树状图的方法求小明、小丽都参加实验A考查的概率;
(3)他们三人都参加实验A考查的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】 (x-2)(x+1)=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个机器人从点O出发,向正西方向走2m到达点A1;再向正北方向走4m到达点A2,再向正东方向走6m到达点A3,再向正南方向走8m到达点A4,再向正东方向走10m到达点A5,…按如此规律走下去,当机器人走到点A2017时,点A2017的坐标为( )

A. (2016,2016) B. (2016,-2016) C. (-2018,-2016) D. (-2018,2020)
-
科目: 来源: 题型:
查看答案和解析>>【题目】 因式分解:a3b-2a2b2+ab3.
相关试题

