【题目】如图,在平面直角坐标系中,已知点![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按顺时针方向旋转得到
按顺时针方向旋转得到![]() ,使
,使![]() 所在直线经过点
所在直线经过点![]() ,则直线
,则直线![]() 的解析式为__________.
的解析式为__________.

参考答案:
【答案】![]()
【解析】
作DE垂直于x轴,DF垂直于y轴,根据勾股定理求出BO,根据旋转性质和等腰三角形性质得AB=AC,∠ADC=90°,BD=CD,设D(x,y),根据勾股定理得 ,再根据待定系数法求解.
,再根据待定系数法求解.
作DE垂直于x轴,DF垂直于y轴
在Rt△ABO中,BO=![]()
由旋转性质可得AB=AC,∠ADC=90°
又因为![]() 所在直线经过点
所在直线经过点![]() ,
,
所以BD=CD
设D(x,y)
根据勾股定理可得

即
①-②,得
-6x+8y=0
所以![]() ③
③
把③代入①,得
![]()
解得![]() 或x=0(舍去)
或x=0(舍去)
把![]() 代入③得
代入③得
![]()
所以D(![]() ,
,![]() )
)
设直线![]() 的解析式为y=kx+4,则
的解析式为y=kx+4,则
![]()
解得![]()
所以![]()
故答案为:![]()

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边
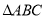 的边长为3,点
的边长为3,点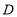 为
为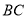 边上一点,且
边上一点,且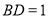 ,
,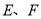 分别为边
分别为边 上的点(不包括端点),则
上的点(不包括端点),则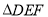 周长的最小值为( )
周长的最小值为( )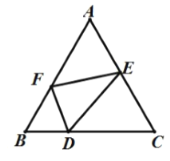
A.
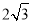 B.
B.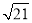 C.
C.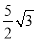 D.
D.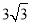
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班参加一次智力竞赛,共a、b、c三题,每题或者得满分或者得0分,其中题a满分20分,题b、题c满分均为25分.竞赛结果,每个学生至少答对了一题,三题全答对的有1人,答对其中两道题的有15人,答对题a的人数与答对题b的人数之和为29,答对题a的人数与答对题c的人数之和为25,答对题b的人数与答对题c的人数之和为20,在这个班的平均成绩是__分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:善于思考的小军在解方程组
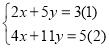 时,采用了一种“整体代换”的解法,
时,采用了一种“整体代换”的解法,解:将方程②变形:4x+10y+y=5即2(2x+5y)+y=5③,把方程①代入③得:2×3+y=5,y=﹣1,把y=﹣1代入①得x=4,所以,方程组的解为
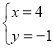 .
.请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组
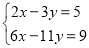 .
.(2)已知x,y满足方程组
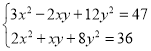 ,求x2+4y2﹣xy的值.
,求x2+4y2﹣xy的值. -
科目: 来源: 题型:
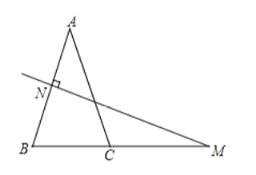
查看答案和解析>>【题目】在
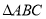 中,
中,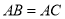 ,
,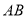 的垂直平分线交
的垂直平分线交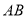 于点
于点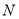 ,交
,交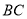 的延长线于点
的延长线于点 .
.(1)若
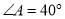 ,则
,则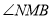 为 度;
为 度;(2)如果
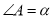 (
(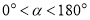 ),其余条件不变,求
),其余条件不变,求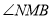 的度数;
的度数;(3)补全规律:等腰三角形一腰的垂直平分线与 相交所成的锐角等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,求证:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等;
(2)如图2,若
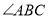 的平分线与
的平分线与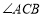 外角
外角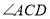 的平分线相交于点
的平分线相交于点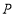 连接
连接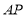 ,若
,若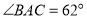 ,则
,则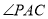 是 度.
是 度.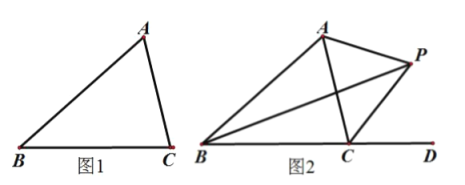
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校“阳光足球俱乐部”计划购进一批甲、乙两种型号的足球,乙型足球每个进价比甲型足球每个进价多10元,若购进甲型足球3个和乙型足球5个,共需要资金370元.
(1)求甲、乙两种型号的足球进价各是多少元?
(2)该商店计划购进这两种型号的足球共50个,而可用于购买这两种型号的足球资金不少于2250元,但又不超过2270元.该商店有几种进货方案?
(3)已知商店出售一个甲种足球可获利6元,出售一个乙种足球可获利10元,试问在(2)的条件下,商店采用哪种方案可获利最多?
相关试题

