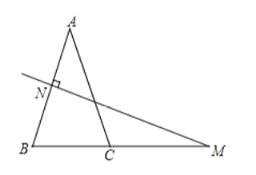
【题目】在![]() 中,
中,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)若![]() ,则
,则![]() 为 度;
为 度;
(2)如果![]() (
(![]() ),其余条件不变,求
),其余条件不变,求![]() 的度数;
的度数;
(3)补全规律:等腰三角形一腰的垂直平分线与 相交所成的锐角等于 .
参考答案:
【答案】(1)20°;(2)![]()
![]() ;(3)底边所在直线,顶角的一半
;(3)底边所在直线,顶角的一半
【解析】
(1)根据等腰三角形性质可得∠B=70°,再根据线段垂直平分线的性质得到∠M=90°-∠B=20°;
(2)与(1)同理,可得∠M=90°-∠B=90°-![]() (180°-
(180°-![]() )=
)=![]()
![]() ;
;
(3)结合(1)(2)可得到:等腰三角形一腰的垂直平分线与底边所在直线相交所成的锐角等于顶角的一半 .
(1)∵∠A=40°,AB=AC,∴∠B=![]() (180°-∠A)=
(180°-∠A)=![]() (180°-40°)=70°,∵MN是AB的垂直平分线,∴MN⊥AB,∴∠M=90°-∠B=90°-70°=20°;
(180°-40°)=70°,∵MN是AB的垂直平分线,∴MN⊥AB,∴∠M=90°-∠B=90°-70°=20°;
(2)如果![]() (
(![]() ),
),
∵![]() ,AB=AC,∴∠B=
,AB=AC,∴∠B=![]() (180°-∠A)=
(180°-∠A)=![]() (180°-
(180°-![]() ),∵MN是AB的垂直平分线,∴MN⊥AB,∴∠M=90°-∠B=90°-
),∵MN是AB的垂直平分线,∴MN⊥AB,∴∠M=90°-∠B=90°-![]() (180°-
(180°-![]() )=
)=![]()
![]() ;
;
(3)由(1)和(2)可得规律:等腰三角形一腰的垂直平分线与底边所在直线相交所成的锐角等于顶角的一半 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班参加一次智力竞赛,共a、b、c三题,每题或者得满分或者得0分,其中题a满分20分,题b、题c满分均为25分.竞赛结果,每个学生至少答对了一题,三题全答对的有1人,答对其中两道题的有15人,答对题a的人数与答对题b的人数之和为29,答对题a的人数与答对题c的人数之和为25,答对题b的人数与答对题c的人数之和为20,在这个班的平均成绩是__分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:善于思考的小军在解方程组
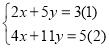 时,采用了一种“整体代换”的解法,
时,采用了一种“整体代换”的解法,解:将方程②变形:4x+10y+y=5即2(2x+5y)+y=5③,把方程①代入③得:2×3+y=5,y=﹣1,把y=﹣1代入①得x=4,所以,方程组的解为
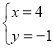 .
.请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组
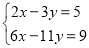 .
.(2)已知x,y满足方程组
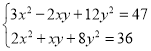 ,求x2+4y2﹣xy的值.
,求x2+4y2﹣xy的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点
 分别在
分别在 轴、
轴、 轴的正半轴上,
轴的正半轴上, ,
, ,将
,将 绕点
绕点 按顺时针方向旋转得到
按顺时针方向旋转得到 ,使
,使 所在直线经过点
所在直线经过点 ,则直线
,则直线 的解析式为__________.
的解析式为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,求证:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等;
(2)如图2,若
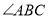 的平分线与
的平分线与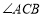 外角
外角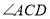 的平分线相交于点
的平分线相交于点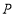 连接
连接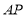 ,若
,若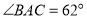 ,则
,则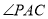 是 度.
是 度.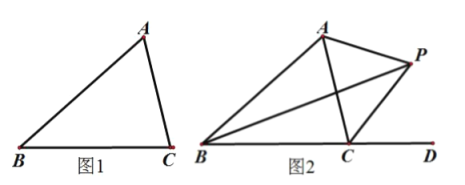
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校“阳光足球俱乐部”计划购进一批甲、乙两种型号的足球,乙型足球每个进价比甲型足球每个进价多10元,若购进甲型足球3个和乙型足球5个,共需要资金370元.
(1)求甲、乙两种型号的足球进价各是多少元?
(2)该商店计划购进这两种型号的足球共50个,而可用于购买这两种型号的足球资金不少于2250元,但又不超过2270元.该商店有几种进货方案?
(3)已知商店出售一个甲种足球可获利6元,出售一个乙种足球可获利10元,试问在(2)的条件下,商店采用哪种方案可获利最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.
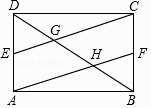
求证:
(1)四边形AFCE是平行四边形;
(2)证明:EG=FH.
相关试题

