【题目】如图,△ABC内接于⊙O,点D在半径OB的延长线上,∠BCD=∠A=30°. 
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径长为1,求由弧BC、线段CD和BD所围成的阴影部分面积.(结果保留π和根号)
参考答案:
【答案】
(1)解:直线CD与⊙O相切,
∵在⊙O中,∠COB=2∠CAB=2×30°=60°,
又∵OB=OC,
∴△OBC是正三角形,
∴∠OCB=60°,
又∵∠BCD=30°,
∴∠OCD=60°+30°=90°,
∴OC⊥CD,
又∵OC是半径,
∴直线CD与⊙O相切.
(2)解:由(1)得△OCD是Rt△,∠COB=60°,
∵OC=1,
∴CD= ![]() ,
,
∴S△COD= ![]() OCCD=
OCCD= ![]() ,
,
又∵S扇形OCB= ![]() ,
,
∴S阴影=S△COD﹣S扇形OCB= ![]() .
.
【解析】(1)由已知可证得OC⊥CD,OC为圆的半径所以直线CD与⊙O相切;(2)根据已知可求得OC,CD的长,则利用S阴影=S△COD﹣S扇形OCB求得阴影部分的面积.
【考点精析】本题主要考查了切线的判定定理的相关知识点,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).点D在线段PQ上,且PD=PC.

(1)求证:PQ∥AB;
(2)若点D在∠BAC的平分线上,求CP的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=AC,CD⊥AB于D.
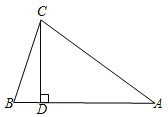
(1)若∠A=38,求∠DCB的度数;
(2)若AB=5,CD=3,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中小方格边长为1,请你根据所学的知识解决下面问题.
(1)求网格图中△ABC的面积.
(2)判断△ABC是什么形状?并所明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间 x(单位:h)变化的图象如图所示,

根据图中提供的信息,有下列说法:①两人相遇前,甲的速度小于乙的速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙多3km;④甲比乙先到达终点.其中正确的有____个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农庄计划在30亩空地上全部种植蔬菜和水果,菜农小张和果农小李分别承包了种植蔬菜和水果的任务,小张种植每亩蔬菜的工资y(元)与种植面积m(亩)之间的函数关系如图①所示,小李种植水果所得报酬z(元)与种植面积n(亩)之间的函数关系如图②所示

(1)如果种植蔬菜20亩,则小张种植每亩蔬菜的工资是元,小张应得的工资总额是元,此时,小李种植水果亩,小李应得的报酬是元;
(2)设农庄支付给小张和小李的总费用为W(元),当10<m<30时,求W与m之间的函数关系式,并求出总费用最大为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.
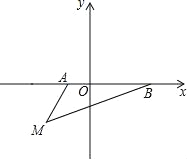
(1)填空:a= ,b= ;
(2)如果在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=
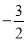 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
相关试题

