【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.
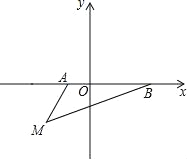
(1)填空:a= ,b= ;
(2)如果在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=![]() 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
参考答案:
【答案】(1)a=-1,b=3;
(2)S△ABM=-2m
(3)P点坐标为(0, ![]() )或(7,0)或(0,
)或(7,0)或(0, ![]() )
)
【解析】试题分析:(1)根据非负数的意义,可直接求出求出a、b的值;
(2)作MC⊥AB于C,由M点在第三象限,可结合头像变化,然后再讨论,根据三角形的面积求解出三角形的面积即可;
(3)根据题意,可分为在x轴上或y轴上,然后根据割补法求三角形的面积,确定点的坐标.
试题解析:
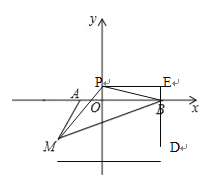
解:(1)填空:a=-1 ,b= 3 ;
(2)作MC⊥AB于C,
由点M(﹣2,m)在第三象限,则MC=|m|=-m,
又A(-1,0),B(3,0),则AB=4,
S△ABM=0.5×AB×MC=0.5×4×(-m)=-2m
(3)由m=![]() ,则S△ABM=-2m=3,
,则S△ABM=-2m=3,
当P在x轴上时,S△pBM=S△ABM即![]() ,因此
,因此
BP=AB=4,因此点P的坐标为(7,0);
当P在y轴的正半轴时,如图,S△pBM=S△ABM=3,分别过点P、B、M作PE∥x轴,MD∥x轴,DE∥y轴,
令点P(0,n)则PE=3,BE=n,ED=n+![]() ,BD=
,BD=![]() ,MD=5,由S梯形MDEP= S△pBM + S△DBM + S△pBE
,MD=5,由S梯形MDEP= S△pBM + S△DBM + S△pBE
即,解得n=0.3,则P(0,![]() )
)
当P在y轴负半轴且在MB下方时,求得P(0.,![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,点D在半径OB的延长线上,∠BCD=∠A=30°.

(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径长为1,求由弧BC、线段CD和BD所围成的阴影部分面积.(结果保留π和根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间 x(单位:h)变化的图象如图所示,

根据图中提供的信息,有下列说法:①两人相遇前,甲的速度小于乙的速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙多3km;④甲比乙先到达终点.其中正确的有____个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农庄计划在30亩空地上全部种植蔬菜和水果,菜农小张和果农小李分别承包了种植蔬菜和水果的任务,小张种植每亩蔬菜的工资y(元)与种植面积m(亩)之间的函数关系如图①所示,小李种植水果所得报酬z(元)与种植面积n(亩)之间的函数关系如图②所示

(1)如果种植蔬菜20亩,则小张种植每亩蔬菜的工资是元,小张应得的工资总额是元,此时,小李种植水果亩,小李应得的报酬是元;
(2)设农庄支付给小张和小李的总费用为W(元),当10<m<30时,求W与m之间的函数关系式,并求出总费用最大为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
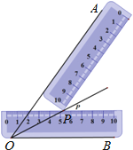
A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 三角形三条垂直平分线的交点到三个定点的距离相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.

(1)当∠BDA=115°时,∠BAD= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中BA=BC,点D是AB延长线上一点,DF⊥AC于F交BC于E,
求证:△DBE是等腰三角形.

相关试题

