【题目】已知一次函数y=﹣ ![]() x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.
x+6的图象与坐标轴交于A、B点(如图),AE平分∠BAO,交x轴于点E.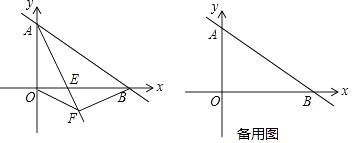
(1)求点B的坐标;
(2)求直线AE的表达式;
(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB的面积.
参考答案:
【答案】
(1)解:当y=﹣ ![]() x+6=0时,x=8,
x+6=0时,x=8,
∴点B的坐标为(8,0).
(2)解:当x=0时,y=﹣ ![]() x+6=6,
x+6=6,
∴点A的坐标为(0,6),
∴OA=6,OB=8,
∴AB= ![]() =10.
=10.
∵AE平分∠BAO,交x轴于点E,
∴ ![]() =
= ![]() ,
,
∴OE= ![]() BE.
BE.
∵OE+BE=OB=8,
∴OE=3,BE=5,
∴点E的坐标为(3,0).
设直线AE的表达式为y=kx+b,
将A(0,6)、E(3,0)代入y=kx+b,
![]() ,解得:
,解得: ![]() ,
,
∴直线AE的表达式为y=﹣2x+6.
(3)解:过点F作FG⊥x轴于点G,如图所示.
∵BF⊥AE,
∴∠BFE=90°=∠AOE.
∵∠AEO=∠BEF,
∴△AOE∽△BFE,
∴ ![]() =
= ![]() =
= ![]() .
.
∵OA=6,OE=3,
∴AE=3 ![]() .
.
∵BE=5,
∴BF=2 ![]() ,EF=
,EF= ![]() .
.
同理可得:△BEF∽△BFG,
∴BG=4,FG=2.
∵OB=8,
∴OG=4=BG,
∴△OFB为等腰三角形,
∴S△OFB= ![]() OBFG=8.
OBFG=8.
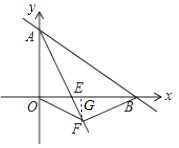
【解析】(1)将y=0代入直线AB的表达式中求出x值,此题得解;(2)利用一次函数图象上点的坐标特征求出点A的坐标,结合勾股定理可求出AB的长度,再利用角平分线的性质即可求出点E的坐标,根据点A、E的坐标利用待定系数法即可求出直线AE的表达式;(3)过点F作FG⊥x轴于点G,由BF⊥AE可得出△AOE∽△BFE,根据相似三角形的性质可得出BF、EF的长度,同理可得出△BEF∽△BFG,根据相似三角形的性质可得出BG、FG的长度,结合OB=8即可得出OG=BG,由此可得出△OFB为等腰三角形,再根据三角形的面积公式可得出△OFB的面积.
【考点精析】掌握相似三角形的性质是解答本题的根本,需要知道对应角相等,对应边成比例的两个三角形叫做相似三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线y=
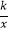 的一部分,请根据图中信息解答下列问题:
的一部分,请根据图中信息解答下列问题: 
(1)求k的值;
(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC和△A1B1C1关于点E成中心对称.

(1)画出对称中心E,并写出点E、A、C的坐标;
(2)P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P2(a+6,b+2),请画出上述平移后的△A2B2C2,并写出点A2、C2的坐标;
(3)判断△A2B2C2和△A1B1C1的位置关系(直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在平面直角坐标系中,
 OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+b将
OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+b将 OABC的面积平分,则b=_______.
OABC的面积平分,则b=_______.(2)在平面直角坐标系中,直线y=2x+3关于原点对称的直线的表达式为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5.OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
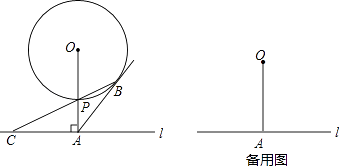
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=2 ,求⊙O的半径和线段PB的长;
,求⊙O的半径和线段PB的长;
(3)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围. -
科目: 来源: 题型:
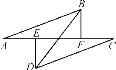
查看答案和解析>>【题目】如图,点A,E,F,C在一条直线上,若将△DEC的边EC沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于点E,BF⊥AC于点F,且AB=CD.则当点E,F不重合时,BD与EF的关系是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分8分)某厂制作甲、乙两种环保包装盒。已知同样用6m的材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制作一个乙盒需要多用20%的材料。
(1)求制作每个甲盒、乙盒各用多少材料?
(2)如果制作甲、乙两种包装盒3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需材料总长度
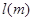 与甲盒数量
与甲盒数量 之间的函数关系式,并求出最少需要多少米材料。
之间的函数关系式,并求出最少需要多少米材料。
相关试题

