【题目】如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.
(1)当△CDQ≌△CPQ时,求AQ的长;
(2)取CQ的中点M,连接MD,MP,若MD⊥MP,求AQ的长.

参考答案:
【答案】(1)![]() (2)2
(2)2
【解析】试题分析:(1)由全等三角形的性质得到DQ=PQ,PC=DC=5,然后利用勾股定理求解即可;
(2)过M作EF⊥CD于F,则EF⊥AB,先证得△MDF≌△PME,得出ME=DF=![]() ,然后用梯形的中位线的性质定理求解即可.
,然后用梯形的中位线的性质定理求解即可.
试题解析:(1)∵△CDQ≌△CPQ,∴DQ=PQ,PC=DC,∵AB=DC=5,AD=BC=3,∴PC=5,在RT△PBC中,PB=![]() =4,∴PA=AB﹣PB=5﹣4=1,设AQ=x,则DQ=PQ=3﹣x,在RT△PAQ中,
=4,∴PA=AB﹣PB=5﹣4=1,设AQ=x,则DQ=PQ=3﹣x,在RT△PAQ中,![]() ,解得x=
,解得x=![]() ,∴AQ=
,∴AQ=![]() .
.
(2)如图2,过M作EF⊥CD于F,则EF⊥AB,∵MD⊥MP,∴∠PMD=90°,∴∠PME+∠DMF=90°,∵∠FDM+∠DMF=90°,∴∠MDF=∠PME,∵M是QC的中点,根据直角三角形直线的性质求得DM=PM=![]() QC,在△MDF和△PME中,∵∠MDF=∠PME,∠DFM=∠MEP,DM=PM,∴△MDF≌△PME(AAS),∴ME=DF,PE=MF,∵EF⊥CD,AD⊥CD,∴EF∥AD,∵QM=MC,∴DF=CF=
QC,在△MDF和△PME中,∵∠MDF=∠PME,∠DFM=∠MEP,DM=PM,∴△MDF≌△PME(AAS),∴ME=DF,PE=MF,∵EF⊥CD,AD⊥CD,∴EF∥AD,∵QM=MC,∴DF=CF=![]() DC=
DC=![]() ,∴ME=
,∴ME=![]() ,∵ME是梯形ABCQ的中位线,∴2ME=AQ+BC,即5=AQ+3,∴AQ=2.
,∵ME是梯形ABCQ的中位线,∴2ME=AQ+BC,即5=AQ+3,∴AQ=2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】节约用水是我们的美德,水龙头关闭不严会造成滴水,容器内盛水
 与滴水时间
与滴水时间 的关系用可以显示水量的容器做如图
的关系用可以显示水量的容器做如图 的试验,并根据试验数据绘制出如图
的试验,并根据试验数据绘制出如图 的函数图象,结合图象解答下列问题.
的函数图象,结合图象解答下列问题.(
 )容器内原有水多少升.
)容器内原有水多少升.(
 )求
)求 与
与 之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.
之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,对角线AC、BD交于点O,点E是BC上一点,且AB=BE,∠1=15°,则∠2=________°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,林老师给出了下列方框中的一道题:
小聪和同桌小明讨论后,得出如下解答:
(
 )特殊情况,探索结论
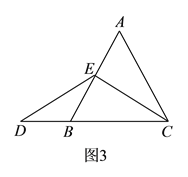
)特殊情况,探索结论当点
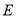 为
为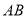 的中点时,如图
的中点时,如图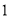 ,确定线段
,确定线段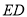 与
与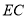 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论: 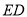 ______
______ 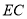 (填“
(填“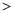 ”“
”“ 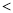 ”或“
”或“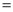 ”).
”).(
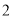 )特例启发,解答问题
)特例启发,解答问题解:题目中,
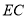 与
与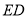 的大小关系是
的大小关系是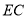 __________
__________ 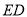 (填“
(填“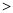 ”“
”“ 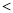 ”或“
”或“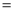 ”),理由如下:如图
”),理由如下:如图 ,过点
,过点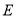 作
作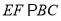 ,交
,交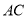 于点
于点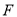 ,(请你继续完成接下来的解题过程).
,(请你继续完成接下来的解题过程).(
 )拓展讨论,设计新题
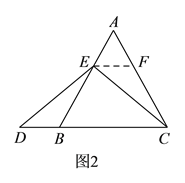
)拓展讨论,设计新题①互换林老师所给题的条件和结论,即:如图
 在等边三角形
在等边三角形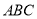 中,点
中,点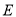 在
在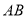 上,点
上,点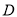 在
在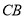 的延长线上,且
的延长线上,且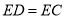 ,试确定线段
,试确定线段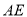 与
与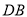 的大小关系,并说明理由.
的大小关系,并说明理由.②在等边三角形
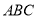 中,点
中,点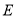 在直线
在直线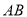 上,点
上,点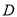 在直线
在直线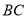 上,且
上,且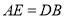 ,若
,若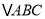 的边长为
的边长为 ,
, 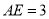 ,求
,求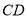 的长为__________(请你直接写出结果).
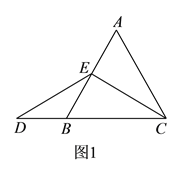
的长为__________(请你直接写出结果).如图,在等边三角形
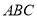 中,点
中,点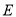 在
在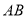
上,点
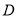 在
在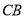 的延长线上,且
的延长线上,且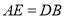 ,
,试确定线段
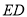 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.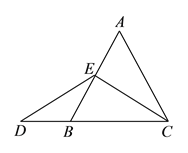
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AC∥BD,连接AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角)

(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答成立或不成立)
(3)当动点P落在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点P的具体位置和相应的结论.选择其中一种结论加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,已知等腰
,已知等腰 在平面直角坐标系中,顶点
在平面直角坐标系中,顶点 在
在 轴上,直角顶点
轴上,直角顶点 在
在 轴上,点
轴上,点 的坐标为
的坐标为 ,直线
,直线 的解析式为
的解析式为 .
.(
 )求直线
)求直线 的函数解析式.
的函数解析式.(
 )如图
)如图 ,直线
,直线 交
交 轴于
轴于 ,延长
,延长 至点
至点 ,使
,使 ,连结
,连结 ,求证:
,求证:  .
.(
 )如图
)如图 ,直线
,直线 交
交 轴于
轴于 ,已知点
,已知点 的坐标为
的坐标为 ,在直线
,在直线 上是否存在一点
上是否存在一点 ,使
,使 的面积是
的面积是 面积的
面积的 ,若存在,请求出点
,若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.


相关试题

