【题目】数学课上,林老师给出了下列方框中的一道题:
小聪和同桌小明讨论后,得出如下解答:
(![]() )特殊情况,探索结论
)特殊情况,探索结论
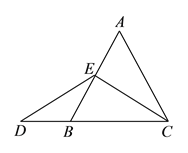
当点![]() 为
为![]() 的中点时,如图
的中点时,如图![]() ,确定线段
,确定线段![]() 与
与![]() 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论: ![]() ______
______ ![]() (填“
(填“![]() ”“
”“ ![]() ”或“
”或“![]() ”).
”).
(![]() )特例启发,解答问题
)特例启发,解答问题
解:题目中, ![]() 与
与![]() 的大小关系是
的大小关系是![]() __________
__________ ![]() (填“
(填“![]() ”“
”“ ![]() ”或“
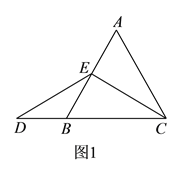
”或“![]() ”),理由如下:如图
”),理由如下:如图![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,(请你继续完成接下来的解题过程).
,(请你继续完成接下来的解题过程).
(![]() )拓展讨论,设计新题
)拓展讨论,设计新题
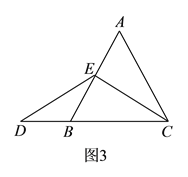
①互换林老师所给题的条件和结论,即:如图![]() 在等边三角形
在等边三角形![]() 中,点
中,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,试确定线段
,试确定线段![]() 与
与![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
②在等边三角形![]() 中,点
中,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() ,若
,若![]() 的边长为
的边长为![]() ,
, ![]() ,求
,求![]() 的长为__________(请你直接写出结果).
的长为__________(请你直接写出结果).
如图,在等边三角形![]() 中,点
中,点![]() 在
在![]()
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,
,
试确定线段![]() 与
与![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
参考答案:
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ,见解析;(
,见解析;(![]() )①
)①![]() ;②
;②![]() 或
或![]() .
.
【解析】试题分析:(1)根据△ABC是等边三角形,点E为AB的中点,即可得出CE⊥AB,进而得出∠ECD=∠D,即可得出线段ED与EC的大小关系;
(2)首先得出BE=CF,进而利用△DBE≌△EFC即可得出答案;
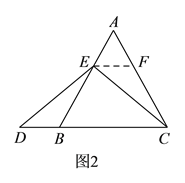
(3)①作![]() ,交
,交![]() 于点
于点![]() ,可知
,可知![]() 为等边三角形,进而证明
为等边三角形,进而证明![]() ≌
≌![]() ,即可得出
,即可得出![]() ;
;
②分点D在CB的延长线上、在BC的延长线上两种情况进行讨论即可得.
试题解析:(![]() )
)![]() .
.
∵![]() 为等边三角形,
为等边三角形, ![]() 是
是![]() 中点,∴
中点,∴![]() ,
, ![]() ,
, ![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
(![]() )
)![]()
在等边![]() 中,
中, ![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
同理![]() ,
,
又在![]() 中,
中, ![]() ,
,
在![]() 中,
中, ![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
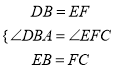 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() .
.
(![]() )①作
)①作![]() ,交
,交![]() 于点
于点![]() ,
,
则可知![]() 为等边三角形,
为等边三角形,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵在![]() 中,
中, ![]() ,
,
在![]() 中,
中, ![]() ,
,
∴![]() ,
,
∴![]() 和
和![]() 中,
中,
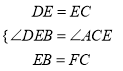 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() .
.
②![]() ,
,
∴![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉兴市某天的最高气温为 8℃,最低气温为 -1℃,则这天嘉兴的最高气温与最低气温差为( )
A.7℃B.8℃C.9℃D.10℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】节约用水是我们的美德,水龙头关闭不严会造成滴水,容器内盛水
 与滴水时间
与滴水时间 的关系用可以显示水量的容器做如图
的关系用可以显示水量的容器做如图 的试验,并根据试验数据绘制出如图
的试验,并根据试验数据绘制出如图 的函数图象,结合图象解答下列问题.
的函数图象,结合图象解答下列问题.(
 )容器内原有水多少升.
)容器内原有水多少升.(
 )求
)求 与
与 之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.
之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,对角线AC、BD交于点O,点E是BC上一点,且AB=BE,∠1=15°,则∠2=________°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.
(1)当△CDQ≌△CPQ时,求AQ的长;
(2)取CQ的中点M,连接MD,MP,若MD⊥MP,求AQ的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AC∥BD,连接AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角)

(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答成立或不成立)
(3)当动点P落在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点P的具体位置和相应的结论.选择其中一种结论加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
相关试题

