【题目】一次函数的图象经过点A(-6,4),B(3,0).
(1)求这个函数的解析式;
(2)画出这个函数的图象;
(3)若该直线经过点(9,m),求m的值;
(4)求△AOB的面积.
参考答案:
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ;(4)6.
;(4)6.
【解析】
(1)利用待定系数法把点A(﹣6,4)B(3,0)代入y=kx+b,可得关于k、b的方程组,再解出方程组可得k、b的值,进而得到函数解析式;
(2)根据题意作出图象即可;
(3)把(9,m)代入y=2x﹣2,即可求得m的值;
(4)根据三角形的面积公式即可得到结论.
(1)设一次函数为:y=kx+b.
∵一次函数的图象经过点A(﹣6,4)B(3,0),∴![]() ,解得:
,解得: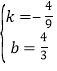
∴这个一次函数的表达式为y=﹣![]() x+
x+![]() ;
;
(2)图象如图所示;
(3)把(9,m)代入y=﹣![]() x+
x+![]() ,得:m=﹣
,得:m=﹣![]() ;
;
(4)连接OA,则S△AOB=![]() ×3×4=6.
×3×4=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,点A、B、C、D在一条直线上,填写下列空格:
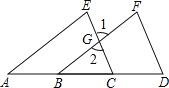
因为∠1=∠E(已知),所以______ // ______ .
因为CE//DF(已知),所以∠1=∠ ______ ,所以∠E=∠ ______ .
(2)说出(1)的推理中应用了哪两个互逆的真命题?
-
科目: 来源: 题型:
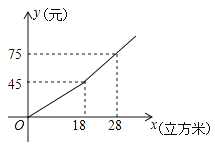
查看答案和解析>>【题目】某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准,该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.
(1)若某月用水量为18立方米,则应交水费多少元?
(2)求当x>18时,y关于x的函数表达式,若小敏家某月交水费81元,则这个月用水量为多少立方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=(2m+3)x+m-1.
(1)若函数图象经过原点,求m的值;
(2)若函数图象与y轴上的的交点位于原点上方,求m的取值范围;
(3)若函数图象平行于直线y=x+1,求m的值;
(4)若该函数的值y随自变量x的增大而减小,求m的取值范围.
-
科目: 来源: 题型:
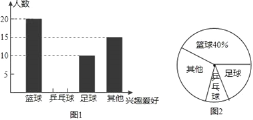
查看答案和解析>>【题目】为响应国家要求中小学生每天锻炼1小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对某班同学参加锻炼的情况进行了统计,并绘制了图1和图2的统计图.请回答下列问题:
(1)该班共有多少名学生?
(2)求图1中“乒乓球”部分的人数,并在图1中将“乒乓球”部分的图形补充完整;
(3)求出扇形统计图中表示“足球”的扇形的圆心角度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.
已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:(A组:x<155;B组:155≤x<160;C组:160≤x<165;D组165≤x<170;E组:x≥170)
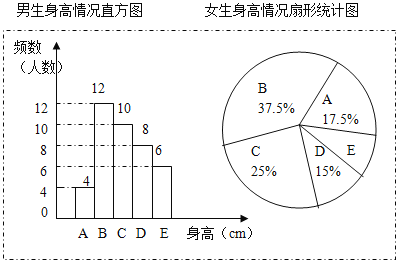
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在 组,中位数在 组.
(2)样本中,女生的身高在E组的人数有 人.
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题。
端午节期间,某食堂根据职工食用习惯,用700元购进甲、乙两种粽子260个,其中甲种粽子比乙种粽子少用100元,已知甲种粽子单价比乙种粽子单价高20%,乙种粽子的单价是多少元?甲、乙两种粽子各购买了多少个?
相关试题

