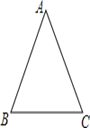
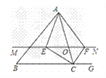
【题目】如图,已知在△ABC中,AB=AC.
(1)试用直尺和圆规在AC上找一点D,使AD=BD(不写作法,但需保留作图痕迹).
(2)在(1)中,连接BD,若BD=BC,求∠A的度数.
参考答案:
【答案】 (1) 作图见解析;(2)36°.
【解析】试题分析:(1)直接利用线段垂直平分线的性质得出符合题意的图形;
(2)直接利用等腰三角形的性质结合三角形内角和定理得出答案.
试题解析:(1)如图所示:
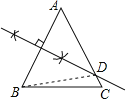
(2)设∠A=x,
∵AD=BD,
∴∠DBA=∠A=x,
在△ABD中
∠BDC=∠A+∠DBA=2x,
又∵BD=BC,
∴∠C=∠BDC=2x,
又∵AB=AC,
∴∠ABC=∠C=2x,
在△ABC中
∠A+∠ABC+∠C=180°,
∴x+2x+2x=180°,
∴x=36°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果某三角形的两边长分别为5和7,第三边的长为偶数,那么这个三角形的周长可以是( )
A. 14 B. 17 C. 22 D. 26
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2+3x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:每购买500元商品,就能获得一次转动转盘的机会,如果转盘停止后,指针上对准500、200、100、50、10的区域,顾客就可以获得500元、200元、100元、50元、10元的购物券一张(转盘等分成20份)。
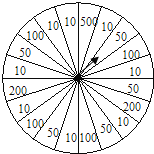
(1)小华购物450元,他获得购物券的概率是多少?
(2)小丽购物600元,那么:
① 她获得50元购物券的概率是多少?
② 她获得100元以上(包括100元)购物券的概率是多少?
-
科目: 来源: 题型:
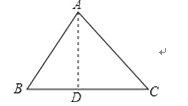
查看答案和解析>>【题目】一、阅读理解:
在△ABC中,BC=a,CA=b,AB=c;
(1)若∠C为直角,则a2+b2=c2;
(2)若∠C为锐角,则a2+b2与c2的关系为:a2+b2>c2;
(3)若∠C为钝角,试推导a2+b2与c2的关系.
二、探究问题:在△ABC中,BC=a=3,CA=b=4,AB=c,若△ABC是钝角三角形,求第三边c的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角∠ACG平分线于点F.
(1)试说明EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并说明理由.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF 是正方形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市因水而名,因水而美,因水而兴,市政府作出了“五水共治”决策:治污水、防洪水、排涝水、保供水、抓节水.某区某乡镇对某河道进行整治,由甲乙两工程队合作20天可完成.已知甲工程队单独整治需60天完成.
(1)求乙工程队单独完成河道整治需多少天?
(2)若甲乙两工程队合做a天后,再由甲工程队单独做 天(用含a的代数式表示)可完成河道整治任务.
(3)如果甲工程队每天施工费5000元,乙工程队每天施工费为1.5万元,先由甲乙两工程队合作整治,剩余工程由甲工程队单独完成,问要使支付两工程队费用最少,并且确保河道在40天内(含40天)整治完毕,问需支付两工程队费用最少多少万元?
相关试题

