【题目】某市因水而名,因水而美,因水而兴,市政府作出了“五水共治”决策:治污水、防洪水、排涝水、保供水、抓节水.某区某乡镇对某河道进行整治,由甲乙两工程队合作20天可完成.已知甲工程队单独整治需60天完成.
(1)求乙工程队单独完成河道整治需多少天?
(2)若甲乙两工程队合做a天后,再由甲工程队单独做 天(用含a的代数式表示)可完成河道整治任务.
(3)如果甲工程队每天施工费5000元,乙工程队每天施工费为1.5万元,先由甲乙两工程队合作整治,剩余工程由甲工程队单独完成,问要使支付两工程队费用最少,并且确保河道在40天内(含40天)整治完毕,问需支付两工程队费用最少多少万元?
参考答案:
【答案】(1)乙工程队单独完成河道整治需30天;;
(2)(60﹣3a);
(3)最少费用为35万元.
【解析】
试题分析:(1)设乙工程队单独完成河道整治需x天,根据工作量为“1”列出方程并解答;
(2)设甲工程队单独做x天,根据甲的工作量+乙的工作量=1列出方程并解答;
(3)利用(2)的结果求得a的取值范围.设费用为y,则由总费用=甲施工费+乙施工费列出方程并解答.
试题解析:(1)设乙工程队单独完成河道整治需x天,
依题意得:![]() ,
,
解得x=30.
经检验,x=30是原方程的根并符合题意.
答:乙工程队单独完成河道整治需30天;
(2)设甲工程队单独做x天,
依题意得:![]() ,
,
解得x=60﹣3a.
故答案是:(60﹣3a);
(3)由(2)得,一共用了a+60﹣3a=60﹣2a≤40,a≥10.
设费用为y,则y=(0.5+1.5)a+0.5(60﹣3a)=0.5a+30.
当a=10时,y最小值为35.
答:最少费用为35万元.
-
科目: 来源: 题型:
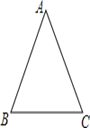
查看答案和解析>>【题目】如图,已知在△ABC中,AB=AC.
(1)试用直尺和圆规在AC上找一点D,使AD=BD(不写作法,但需保留作图痕迹).
(2)在(1)中,连接BD,若BD=BC,求∠A的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一、阅读理解:
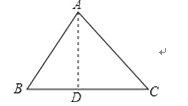
在△ABC中,BC=a,CA=b,AB=c;
(1)若∠C为直角,则a2+b2=c2;
(2)若∠C为锐角,则a2+b2与c2的关系为:a2+b2>c2;
(3)若∠C为钝角,试推导a2+b2与c2的关系.
二、探究问题:在△ABC中,BC=a=3,CA=b=4,AB=c,若△ABC是钝角三角形,求第三边c的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角∠ACG平分线于点F.
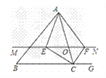
(1)试说明EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并说明理由.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF 是正方形?并说明理由.
-
科目: 来源: 题型:
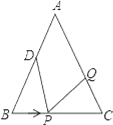
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B向C点运动,同时点Q在线段CA上由C点向A点运动.
(1)若点Q的运动速度与点P的运动速度相等,1秒钟时,△BPD与△CQP是否全等,请说明;
(2)点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD≌△CPQ?
-
科目: 来源: 题型:
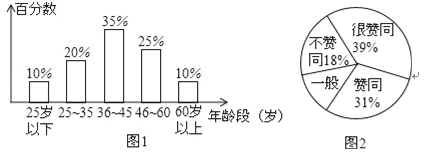
查看答案和解析>>【题目】据报载,在“百万家庭低碳行,垃圾分类要先行”活动中,某地区对随机抽取的1000名公民的年龄段分布情况和对垃圾分类所持态度进行调查,并将调查结果分别绘成条形图(图1)、扇形图(图2).
(1)图2中所缺少的百分数是 ;
(2)这次随机调查中,如果公民年龄的中位数是正整数,那么这个中位数所在年龄段是 ____ (填写年龄段);
(3)这次随机调查中,年龄段是“25岁以下”的公民中“不赞成”的有5名,它占“25岁以下”人数的百分数是 ___ ;
(4)如果把所持态度中的“很赞同”和“赞同”统称为“支持”,那么这次被调查公民中“支持”的人有 ____名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知xa+b=6,xb=3,求xa的值.
相关试题

