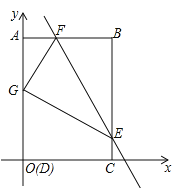
【题目】如图,四边形ABCD为矩形,C点在![]() 轴上,A点在
轴上,A点在![]() 轴上,D(0,0),B(3,4),矩形ABCD沿直线EF折叠,点B落在AD边上的G处,E、F分别在BC、AB边上且F(1,4).
轴上,D(0,0),B(3,4),矩形ABCD沿直线EF折叠,点B落在AD边上的G处,E、F分别在BC、AB边上且F(1,4).
(1)求G点坐标
(2)求直线EF解析式
(3)点N在坐标轴上,直线EF上是否存在点M,使以M、N、F、G为顶点的四边形是平行四边形?若存在,直接写出M点坐标;若不存在,请说明理由
参考答案:
【答案】(1)G(0,4-![]() );(2)
);(2)![]() ;(3)
;(3) .
.
【解析】
1(1)由F(1,4),B(3,4),得出AF=1,BF=2,根据折叠的性质得到GF=BF=2,在Rt△AGF中,利用勾股定理求出![]() ,那么OG=OA-AG=4-
,那么OG=OA-AG=4-![]() ,于是G(0,4-
,于是G(0,4-![]() );
);
(2)先在Rt△AGF中,由![]() ,得出∠AFG=60°,再由折叠的性质得出∠GFE=∠BFE=60°,解Rt△BFE,求出BE=BF
,得出∠AFG=60°,再由折叠的性质得出∠GFE=∠BFE=60°,解Rt△BFE,求出BE=BF![]() tan60°=2
tan60°=2![]() ,那么CE=4-2
,那么CE=4-2![]() ,E(3,4-2
,E(3,4-2![]() ).设直线EF的表达式为y=kx+b,将E(3,4-2
).设直线EF的表达式为y=kx+b,将E(3,4-2![]() ),F(1,4)代入,利用待定系数法即可求出直线EF的解析.(3)因为M、N均为动点,只有F、G已经确定,所以可从此入手,结合图形,按照FG为一边,N点在x轴上;FG为一边,N点在y轴上;FG为对角线的思路,顺序探究可能的平行四边形的形状.确定平行四边形的位置与形状之后,利用平行四边形及平移的性质求得M点的坐标.
),F(1,4)代入,利用待定系数法即可求出直线EF的解析.(3)因为M、N均为动点,只有F、G已经确定,所以可从此入手,结合图形,按照FG为一边,N点在x轴上;FG为一边,N点在y轴上;FG为对角线的思路,顺序探究可能的平行四边形的形状.确定平行四边形的位置与形状之后,利用平行四边形及平移的性质求得M点的坐标.
解:(1)∵F(1,4),B(3,4),
∴AF=1,BF=2,
由折叠的性质得:GF=BF=2,
在Rt△AGF中,由勾股定理得,
![]()
∵B(3,4),
∴OA=4,
∴OG=4-![]() ,
,
∴G(0,4-![]() );
);
(2)在Rt△AGF中,
∵![]() ,
,
∴∠AFG=60°,由折叠的性质得知:∠GFE=∠BFE=60°,
在Rt△BFE中,
∵BE=BF![]() tan60°=2
tan60°=2![]() ,
,
.CE=4-2![]() ,
,
.E(3,4-2![]() ).
).
设直线EF的表达式为y=kx+b,
∵E(3,4-2![]() ),F(1,4),
),F(1,4),
∴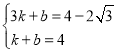 解得
解得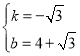
∴![]() ;
;

(3)若以M、N、F、G为顶点的四边形是平行四边形,则分如下四种情况:
①FG为平行四边形的一边,N点在x轴上,GFMN为平行四边形,如图1所示.
过点G作EF的平行线,交x轴于点N1,再过点N:作GF的平行线,交EF于点M,得平行四边形GFM1N1.
∵GN1∥EF,直线EF的解析式为![]()
∴直线GN1的解析式为![]() ,
,
当y=0时,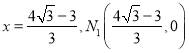 .
.
∵GFM1N1是平行四边形,且G(0,4-![]() ),F(1,4),N1(
),F(1,4),N1(![]() ,0),
,0),
∴M,(![]() ,
,![]() );
);
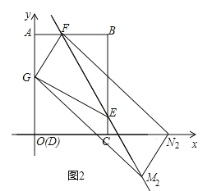
②FG为平行四边形的一边,N点在x轴上,GFNM为平行四边形,如图2所示.
∵GFN2M2为平行四边形,
∴GN与FM2互相平分.
∴G(0,4-![]() ),N2点纵坐标为0
),N2点纵坐标为0
∴GN:中点的纵坐标为![]() ,
,
设GN中点的坐标为(x,![]() ).
).
∵GN2中点与FM2中点重合,
∴![]()
∴x=![]()
∵.GN2的中点的坐标为(![]() ),
),
.∴N2点的坐标为(![]() ,0).
,0).
∵GFN2M2为平行四边形,且G(0,4-![]() ),F(1,4),N2(
),F(1,4),N2(![]() ,0),
,0),
∴M2(![]() );
);

③FG为平行四边形的一边,N点在y轴上,GFNM为平行四边形,如图3所示.
∵GFN3M3为平行四边形,.
∴GN3与FM3互相平分.
∵G(0,4-![]() ),N2点横坐标为0,
),N2点横坐标为0,
.∴GN3中点的横坐标为0,
∴F与M3的横坐标互为相反数,
∴M3的横坐标为-1,
当x=-1时,y=![]() ,
,
∴M3(-1,4+2![]() );
);
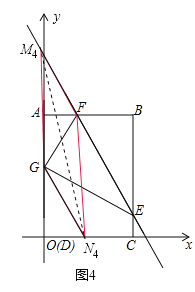
④FG为平行四边形的对角线,GMFN为平行四边形,如图4所示.
过点G作EF的平行线,交x轴于点N4,连结N4与GF的中点并延长,交EF于点M。,得平行四边形GM4FN4
∵G(0,4-![]() ),F(1,4),
),F(1,4),
∴FG中点坐标为(![]() ),
),
∵M4N4的中点与FG的中点重合,且N4的纵坐标为0,
.∴M4的纵坐标为8-![]() .
.
5-45解方程![]() ,得
,得![]()
∴M4(![]() ).
).
综上所述,直线EF上存在点M,使以M,N,F,G为顶点的四边形是平行四边形,此时M点坐标为: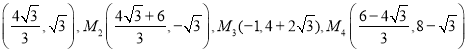 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】有大小两种货车,
 辆大货车与
辆大货车与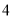 辆小火车一次可以运货
辆小火车一次可以运货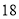 吨,
吨, 辆大货车与
辆大货车与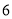 辆小货车一次可以运货
辆小货车一次可以运货 吨.
吨.(1)求
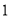 辆大货车和
辆大货车和 辆小货车一次可以分别运多少吨;
辆小货车一次可以分别运多少吨;(2)现有
 吨货物需要运输,货运公司拟安排大小货车共
吨货物需要运输,货运公司拟安排大小货车共 辆把全部货物一次运完.求至少需要安排几辆大货车?
辆把全部货物一次运完.求至少需要安排几辆大货车? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=﹣x+4,回答下列问题:
(1)请在右图的直角坐标系中画出函数y=﹣x+4图象;
(2)y的值随x值的增大而________;
(3)当y=2时,x的值为_________;
(4)当y<0时,x的取值范围是_______.
-
科目: 来源: 题型:
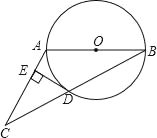
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若∠CAB=120°,⊙O的半径等于5,求线段BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一根起点为1的数轴,现有同学将它弯折,弯折后虚线上第一行的数是1,第二行的数是13,第三行的数是43,…,依此规律,第五行的数是( )

A. 183 B. 157 C. 133 D. 91
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式A=x2+3xy+x-
 ,B=2x2-xy+4y-1
,B=2x2-xy+4y-1(1)当x=y=-2时,求2A-B的值;
(2)若2A-B的值与y的取值无关,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.

(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
相关试题

