【题目】如图,在△ABC中,∠CBD、∠BCE是△ABC的外角,BP平分∠ABC,CP平分∠ACB,BQ平分∠CBD,CQ平分∠BCE.
(1)∠PBQ的度数是 ,∠PCQ的度数是 ;
(2)若∠A=70°,求∠P和∠Q的度数;
(3)若∠A=α,则∠P= ,∠Q= (用含α的代数式表示).

参考答案:
【答案】(1)90°、90°;(2)125°,55°;(3)90°+![]() α、90°﹣
α、90°﹣![]() α.
α.
【解析】
(1)由角平分线知∠PBC=![]() ∠ABC、∠QBC=
∠ABC、∠QBC=![]() ∠DBC,由∠ABC+∠DBC=180°知∠PBQ=∠PBC+∠QBC=
∠DBC,由∠ABC+∠DBC=180°知∠PBQ=∠PBC+∠QBC=![]() (∠ABC+∠DBC)=90°,同理可得∠PCQ的度数;
(∠ABC+∠DBC)=90°,同理可得∠PCQ的度数;
(2)由∠P=180°﹣∠PBC﹣∠PCB=180°﹣![]() ∠ABC﹣
∠ABC﹣![]() ∠ACB=180°﹣
∠ACB=180°﹣![]() (∠ABC+∠ACB)=180°﹣
(∠ABC+∠ACB)=180°﹣![]() (180°﹣∠A)可得∠P度数,由∠Q=180°﹣∠QBC﹣∠QCB=180°﹣
(180°﹣∠A)可得∠P度数,由∠Q=180°﹣∠QBC﹣∠QCB=180°﹣![]() (180°﹣∠ABC)﹣
(180°﹣∠ABC)﹣![]() (180°﹣∠ACB)=
(180°﹣∠ACB)=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°﹣∠A)可得∠Q度数;
(180°﹣∠A)可得∠Q度数;
(3)与(2)同理可得.
(1)∵BP平分∠ABC,CP平分∠ACB,BQ平分∠CBD,CQ平分∠BCE.
∴∠PBC=![]() ∠ABC、∠QBC=
∠ABC、∠QBC=![]() ∠DBC、∠PCB=
∠DBC、∠PCB=![]() ∠ACB、∠QCB=
∠ACB、∠QCB=![]() ∠BCE,
∠BCE,
∵∠ABC+∠DBC=180°、∠ACB+∠BCE=180°,
∴∠PBQ=∠PBC+∠QBC=![]() (∠ABC+∠DBC)=90°,
(∠ABC+∠DBC)=90°,
∠PCQ=∠PCB+∠QCB=![]() (∠ACB+∠BCE)=90°,
(∠ACB+∠BCE)=90°,
故答案为:90°、90°;
(2)∵∠PBC=![]() ∠ABC、∠PCB=
∠ABC、∠PCB=![]() ∠ACB,
∠ACB,
∴∠P=180°﹣∠PBC﹣∠PCB
=180°﹣![]() ∠ABC﹣
∠ABC﹣![]() ∠ACB
∠ACB
=180°﹣![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
=180°﹣![]() (180°﹣∠A)
(180°﹣∠A)
=180°﹣![]() (180°﹣70°)
(180°﹣70°)
=125°;
∵∠QBC=![]() ∠ABC、∠QCB=
∠ABC、∠QCB=![]() ∠ACB,
∠ACB,
∴∠Q=180°﹣∠QBC﹣∠QCB
=180°﹣![]() (180°﹣∠ABC)﹣
(180°﹣∠ABC)﹣![]() (180°﹣∠ACB)
(180°﹣∠ACB)
=![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
=![]() (180°﹣∠A)
(180°﹣∠A)
=![]() (180°﹣70°)
(180°﹣70°)
=55°.
(3)与(2)同理知∠P=180°﹣![]() (180°﹣∠A)=90°+
(180°﹣∠A)=90°+![]() ∠A=90°+
∠A=90°+![]() α,
α,
∠Q=![]() (180°﹣∠A)=90°﹣
(180°﹣∠A)=90°﹣![]() ∠A=90°﹣
∠A=90°﹣![]() α,
α,
故答案为:90°+![]() α、90°﹣
α、90°﹣![]() α.
α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
5台
1800元
第二周
4台
10台
3100元
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
-
科目: 来源: 题型:
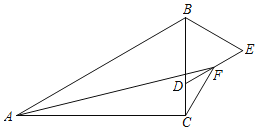
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,AB=4,点D是BC上一动点,以BD为边在BC的右侧作等边△BDE,F是DE的中点,连结AF,CF,则AF+CF的最小值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, ,作斜边AB上中线CD,得到第1个三角形ACD;
,作斜边AB上中线CD,得到第1个三角形ACD; 于点E,作
于点E,作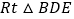 斜边DB上中线EF,得到第2个三角形DEF;依次作下去
斜边DB上中线EF,得到第2个三角形DEF;依次作下去 则第1个三角形的面积等于______,第n个三角形的面积等于______.
则第1个三角形的面积等于______,第n个三角形的面积等于______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=5,线段AB的垂直平分线DE分别交边AB、AC于点E、D.

(1)若∠A=40°,求∠DBC的度数;
(2)若△BCD的周长为8,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在纪念中国抗日战争胜利70周年之际,某公司决定组织员工观看抗日战争题材的影片,门票有甲乙两种,甲种票比乙种票每张贵6元;买甲种票10张,乙种票15张共用去660元.
(1)求甲、乙两种门票每张各多少元?
(2)如果公司准备购买35张门票且购票费用不超过1000元,那么最多可购买多少张甲种票?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,AM∥CN,求证:
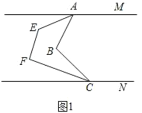

①∠MAB+∠ABC+∠BCN=360°;
②∠MAE+∠AEF+∠EFC+∠FCN=540°;
(2)如图2,若平行线AM与CN间有n个点,根据(1)中的结论写出你的猜想并证明.
相关试题

