【题目】某中学为打造体育特色学校,落实每天锻炼1小时的规定,经调查研究后决定在七、八、九年级分别开展跳绳、羽毛球、毽球项目.七年级共有六个班,每班的人数以![]() 人为标准,各班人数情况如下表.八年级学生人数比七年级学生人数的2倍少240人,九年级学生人数的2倍刚好是七、八年级学生人数的和.(说明:1901班表示七年级一班)
人为标准,各班人数情况如下表.八年级学生人数比七年级学生人数的2倍少240人,九年级学生人数的2倍刚好是七、八年级学生人数的和.(说明:1901班表示七年级一班)
班级 | 1901班 | 1902班 | 1903班 | 1904班 | 1905班 | 1906班 |
与标准人数的(人) | +3 | +2 | -2 | +2 | 0 | -1 |
(1)用含![]() 的代数式表示七年级学生人数.
的代数式表示七年级学生人数.
(2)学校按每人一根跳绳,一个毽球,两人一副羽毛球拍的标准,购买相应的体育器材以满足学生的锻炼需要,已知跳绳每根5元,毽球每个3元,羽毛球拍每副18元,当![]() 时,求购买器材的总费用.
时,求购买器材的总费用.
参考答案:
【答案】(1)![]() 人;(2)购买器材的总费用为4190元.
人;(2)购买器材的总费用为4190元.
【解析】
(1)通过图表可以得到七年级的人数(6a+4)人;
(2)通过(1)得到七年级人数244人,依据题意分别得到八年级和九年级的人数248人和246人,分别根据每个年级所用的体育器材进行计算即可.
解:(1)![]() (人)
(人)
七年级学生人数为![]() 人.
人.
(2)当![]() 时,
时,![]() (人)
(人)
八年级人数:![]() (人)
(人)
九年级人数:![]() (人)
(人)
总费用:![]() (元)
(元)
答:购买器材的总费用为4190元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B分别在x轴、y轴上(OA>OB),以AB为直径的圆经过原点O,C是
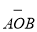 的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有( )
的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有( )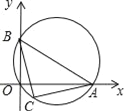
A. 3个 B. 2个 C. 1个 D. 0个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
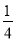 x2+2x的顶点为M,与x轴交于0,A两点,点P(a,0)是线段0A上一动点(不包括端点),过点P作y轴的平行线,交直线y=
x2+2x的顶点为M,与x轴交于0,A两点,点P(a,0)是线段0A上一动点(不包括端点),过点P作y轴的平行线,交直线y=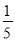 x于点B,交抛物线于点C,以BC为一边,在BC的右侧作矩形BCDE,若CD=2,则当矩形BCDE与△OAM重叠部分为轴对称图形时,a的取值范围是__.
x于点B,交抛物线于点C,以BC为一边,在BC的右侧作矩形BCDE,若CD=2,则当矩形BCDE与△OAM重叠部分为轴对称图形时,a的取值范围是__.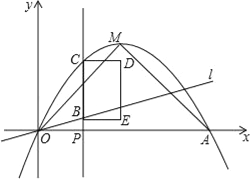
-
科目: 来源: 题型:
查看答案和解析>>【题目】“十年树木,百年树人”,教师的素养关系到国家的未来.我市某区招聘音乐教师采用笔试、专业技能测试、说课三种形式进行选拔,这三项的成绩满分均为100分,并按2∶3∶5的比例纳入总分.最后,按照成绩的排序从高到低依次录取.该区要招聘2名音乐教师,通过笔试、专业技能测试筛选出前6名选手进入说课环节,这6名选手的各项成绩见下表:
序号
1
2
3
4
5
6
笔试成绩/分
66
90
86
64
65
84
专业技能测试成绩/分
95
92
93
80
88
92
说课成绩/分
85
78
86
88
94
85
(1)写出说课成绩的中位数、众数;
(2)已知序号为1,2,3,4号选手的成绩分别为84.2分,84.6分,88.1分,80.8分,请你判断这6名选手中序号是多少的选手将被录用?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品用甲种原料9千克,乙种原料3千克,可获利700元;生产一件B种产品用甲种原料4千克,乙种原料10千克,可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润为y元,其中一种产品生产件数为x件,试写出y与x之间的函数关系式,并利用函数的性质说明那种方案获利最大?最大利润是多少?
-
科目: 来源: 题型:
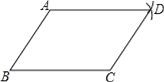
查看答案和解析>>【题目】嘉琪同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的□ABCD,并写出了如下尚不完整的已知和求证.
已知:如图,在四边形ABCD中,BC=AD,AB= .
求证:四边形ABCD是 四边形.
(1)补全已知和求证(在方框中填空);
(2)嘉琪同学想利用三角形全等,依据“两组对边分别平行的四边形是平行四边形”来证明.请你按她的想法完成证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴的正半轴上,反比例函数y=
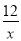 的图象经过点C(3,m).
的图象经过点C(3,m).(1)求菱形OABC的周长;
(2)求点B的坐标.

相关试题

