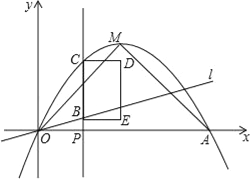
【题目】如图,抛物线y=﹣![]() x2+2x的顶点为M,与x轴交于0,A两点,点P(a,0)是线段0A上一动点(不包括端点),过点P作y轴的平行线,交直线y=
x2+2x的顶点为M,与x轴交于0,A两点,点P(a,0)是线段0A上一动点(不包括端点),过点P作y轴的平行线,交直线y=![]() x于点B,交抛物线于点C,以BC为一边,在BC的右侧作矩形BCDE,若CD=2,则当矩形BCDE与△OAM重叠部分为轴对称图形时,a的取值范围是__.
x于点B,交抛物线于点C,以BC为一边,在BC的右侧作矩形BCDE,若CD=2,则当矩形BCDE与△OAM重叠部分为轴对称图形时,a的取值范围是__.
参考答案:
【答案】![]() 或
或![]() 或
或![]() <a≤5.
<a≤5.
【解析】∵y=﹣![]() x2+2x=﹣
x2+2x=﹣![]() (x﹣4)2+4,∴顶点M的坐标为(4,4),
(x﹣4)2+4,∴顶点M的坐标为(4,4),
令y=0,则﹣![]() x2+2x=0,整理得,x2﹣8x=0,解得x1=0,x2=8,∴点A的坐标为(8,0),
x2+2x=0,整理得,x2﹣8x=0,解得x1=0,x2=8,∴点A的坐标为(8,0),
设直线AM的解析式为y=kx+b(k≠0),则![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=﹣x+8,∴∠MAO=45°,由抛物线的对称性得,△AMO是等腰直角三角形,
①矩形BCDE为正方形时,BC=DC,∴(﹣![]() a2+2a)﹣
a2+2a)﹣![]() a=2,解得a1=
a=2,解得a1=![]() ,a2=
,a2=![]() ;
;
②矩形BCDE关于抛物线对称轴对称时,点P的横坐标a=4+![]() CD=4+
CD=4+![]() ×2=4+1=5;
×2=4+1=5;
③如图,点E在AM上时,设直线y=![]() x与直线AM相交于点G,
x与直线AM相交于点G,
联立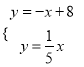 ,解得
,解得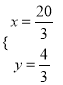 ,∴点G的坐标为(
,∴点G的坐标为(![]() ,
, ![]() ),
),
∵PB∥y轴,四边形BCDE为矩形,∴BE∥x轴,∴△GBE∽△OGA,
∴![]() =
=![]() =
=![]() ,∴
,∴![]() =
=![]() ,
,
过点G作GH⊥x轴于H,则GH∥PB,∴△OBP∽△OGH,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得PB=1,∴点B的纵坐标为1,
,解得PB=1,∴点B的纵坐标为1,
代入y=![]() x得,
x得, ![]() x=1,解得x=5,∴点P的横坐标a=5,
x=1,解得x=5,∴点P的横坐标a=5,
∴从此位置到点B与点G重合,重叠部分为等腰直角三角形,∴![]() <a≤5;
<a≤5;
综上所述,矩形BCDE与△OAM重叠部分为轴对称图形时,a的取值范围是: ![]() 或
或![]() 或5或
或5或![]() <a<5,故答案为
<a<5,故答案为![]() 或
或![]() 或
或![]() <a≤5.
<a≤5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】成语“运筹帷幄”中“筹”的原意是指《孙子算经》中记载的“算筹”.算筹是中国古代用来进行计算的工具,它是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵、横两种形式(如图).
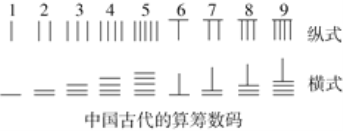
当表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的算筹需要纵、横相间:个位,百位,万位数用纵式表示;十位,千位,十万位数用横式表示:“0”用空位来代替,以此类推,如:数3306用算筹表示成
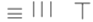 .用算筹
.用算筹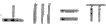 表示的数是______.
表示的数是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】今年假期某校对操场进行了维修改造,如图是操场的一角.在长为
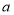 米,宽为
米,宽为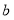 米的长方形场地中间,并排着两个大小相同的篮球场,这两个篮球场之间以及篮球场与长方形场地边沿的距离都为
米的长方形场地中间,并排着两个大小相同的篮球场,这两个篮球场之间以及篮球场与长方形场地边沿的距离都为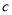 米.
米.(1)直接写出一个篮球场的长和宽;(用含字母
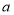 ,
,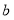 ,
,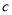 的代数式表示)
的代数式表示)(2)用含字母
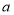 ,
,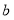 ,
,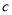 的代数式表示这两个篮球场占地面积的和,并求出当
的代数式表示这两个篮球场占地面积的和,并求出当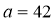 ,
,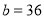 ,
, 时,这两个篮球场占地面积的和.
时,这两个篮球场占地面积的和.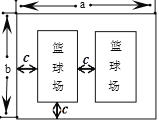
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B分别在x轴、y轴上(OA>OB),以AB为直径的圆经过原点O,C是
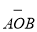 的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有( )
的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有( )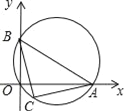
A. 3个 B. 2个 C. 1个 D. 0个
-
科目: 来源: 题型:
查看答案和解析>>【题目】“十年树木,百年树人”,教师的素养关系到国家的未来.我市某区招聘音乐教师采用笔试、专业技能测试、说课三种形式进行选拔,这三项的成绩满分均为100分,并按2∶3∶5的比例纳入总分.最后,按照成绩的排序从高到低依次录取.该区要招聘2名音乐教师,通过笔试、专业技能测试筛选出前6名选手进入说课环节,这6名选手的各项成绩见下表:
序号
1
2
3
4
5
6
笔试成绩/分
66
90
86
64
65
84
专业技能测试成绩/分
95
92
93
80
88
92
说课成绩/分
85
78
86
88
94
85
(1)写出说课成绩的中位数、众数;
(2)已知序号为1,2,3,4号选手的成绩分别为84.2分,84.6分,88.1分,80.8分,请你判断这6名选手中序号是多少的选手将被录用?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为打造体育特色学校,落实每天锻炼1小时的规定,经调查研究后决定在七、八、九年级分别开展跳绳、羽毛球、毽球项目.七年级共有六个班,每班的人数以
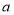 人为标准,各班人数情况如下表.八年级学生人数比七年级学生人数的2倍少240人,九年级学生人数的2倍刚好是七、八年级学生人数的和.(说明:1901班表示七年级一班)
人为标准,各班人数情况如下表.八年级学生人数比七年级学生人数的2倍少240人,九年级学生人数的2倍刚好是七、八年级学生人数的和.(说明:1901班表示七年级一班)班级
1901班
1902班
1903班
1904班
1905班
1906班
与标准人数的(人)
+3
+2
-2
+2
0
-1
(1)用含
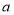 的代数式表示七年级学生人数.
的代数式表示七年级学生人数.(2)学校按每人一根跳绳,一个毽球,两人一副羽毛球拍的标准,购买相应的体育器材以满足学生的锻炼需要,已知跳绳每根5元,毽球每个3元,羽毛球拍每副18元,当
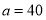 时,求购买器材的总费用.
时,求购买器材的总费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品用甲种原料9千克,乙种原料3千克,可获利700元;生产一件B种产品用甲种原料4千克,乙种原料10千克,可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润为y元,其中一种产品生产件数为x件,试写出y与x之间的函数关系式,并利用函数的性质说明那种方案获利最大?最大利润是多少?
相关试题

