搜索
【题目】如图，菱形ABCD中，对角线AC、BD交于点O，AC=24，BD=10，DE⊥AB于E，
（1）求菱形ABCD的周长；（2）求菱形ABCD的面积；（3）求DE的长.
参考答案：
【答案】（1）52；（2）120；（3）
【解析】试题分析：（1）设AB=x，则BC=x，利用勾股定理求出x的值，即可求出菱形的周长；
（2）首先证明△ADE≌△CDE，在利用勾股定理分别求出BE，DE，进而求出BD，问题得解．根据菱形的对角线互相垂直平分求出OA、OB，再根据勾股定理列式求出AB，然后利用菱形的面积列式计算即可得解．
试题解析：（1）在菱形ABCD中，对角线AC、BD交于点O，
∵AC=24，BD=10
∴AO=12，OD=5
在Rt△AOD中
AD=
∴周长=
（2）S菱形=10×24×
=120
（3）S菱形= 
∴DE·13=120
∴DE=
-
科目： 来源： 题型：
查看答案和解析>>【题目】（10分）感知：如图①，在四边形ABCD中，AB∥CD，∠B=90°，点P在BC边上，当∠APD=90°时，易证△ABP∽△PCD，从而得到BPPC=ABCD（不需证明）
探究：如图②，在四边形ABCD中，点P在BC边上，当∠B=∠C=∠APD时，结论BPPC=ABCD仍成立吗？请说明理由？
拓展：如图③，在△ABC中，点P是BC的中点，点D、E分别在边AB、AC上．若∠B=∠C=∠DPE=45°，BC=4
，CE=3，则DE的长为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】（12分）如图，在平面直角坐标系中，直线
与
轴、
轴分别交于A、B两点，动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动；同时，动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动，当其中一点到达终点时，另一点也随之停止运动．设点P运动的时间为t（秒）．（1）直接写出A、B两点的坐标．
（2）当△APQ与△AOB相似时，求t的值．
（3）设△APQ的面积为S（平方单位），求S与t之间的函数关系式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为拓宽学生视野，引导学生主动适应社会，促进书本知识和生活经验的深度融合，我市某中学决定组织部分班级去赤壁开展研学旅行活动，在参加此次活动的师生中，若每位老师带17个学生，还剩12个学生没人带；若每位老师带18个学生，就有一位老师少带4个学生．现有甲、乙两种大客车，它们的载客量和租金如表所示．
甲种客车
乙种客车
载客量/（人/辆）
30
42
租金/（元/辆）
300
400
学校计划此次研学旅行活动的租车总费用不超过3100元，为了安全，每辆客车上至少要有2名老师．
（1）参加此次研学旅行活动的老师和学生各有多少人？
（2）既要保证所有师生都有车坐，又要保证每辆客车上至少要有2名老师，可知租用客车总数为 辆；
（3）你能得出哪几种不同的租车方案？其中哪种租车方案最省钱？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数
的图象如图所示，点A0位于坐 标原点，点A1，A2，A3，…，A2017在
轴的正半轴上，点B1， B2, B3，…，B2017在二次函数
位于第一象限的图象上，△A0B1A1，△A1B2A2，△A2B3A3，…，△A2016B2017A2017都为等边三角形，则等边△A2016B2017A2017的高为_____.
-
科目： 来源： 题型：
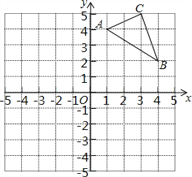
查看答案和解析>>【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，4），B（4，2），C（3，5）（每个方格的边长均为1个单位长度）．
（1）请画出将△ABC向下平移5个单位后得到的△A1B1C1；
（2）将△ABC绕点O逆时针旋转90°，画出旋转后得到的△A2B2C2，并直接写出点A旋转到点A2所经过的路径长．
-
科目： 来源： 题型：
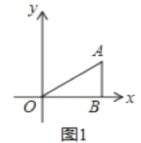
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点O为坐标原点,点A(3a,2a)在第一象限,过点A向x轴作垂线,垂足为点B,连接OA,S△AOB=12，点M从O出发，沿y轴的正半轴以每秒2个单位长度的速度运动，点N从点B出发以每秒3个单位长度的速度向x轴负方向运动，点M与点N同时出发，设点M的运动时间为t秒，连接AM，AN，MN.
(1)求a的值；
(2)当0<t<2时，
①请探究∠ANM，∠OMN，∠BAN之间的数量关系，并说明理由；
②试判断四边形AMON的面积是否变化?若不变化，请求出其值；若变化，请说明理由。
(3)当OM=ON时，请求出t的值。
相关试题
