【题目】(12分)如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
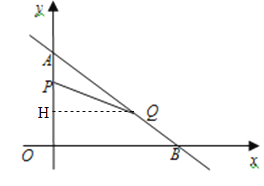
轴、![]() 轴分别交于A、B两点,动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,当其中一点到达终点时,另一点也随之停止运动.设点P运动的时间为t(秒).
轴分别交于A、B两点,动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,当其中一点到达终点时,另一点也随之停止运动.设点P运动的时间为t(秒).
(1)直接写出A、B两点的坐标.
(2)当△APQ与△AOB相似时,求t的值.
(3)设△APQ的面积为S(平方单位),求S与t之间的函数关系式.

参考答案:
【答案】(1)A(0,3),B(4,0);(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)解方程可求得OA、OB的长,容易求得A、B两点的坐标;
(2)由勾股定理可求得AB,用t可表示出AP、QB、AQ的长,分△APQ∽△AOB和△APQ∽△ABO两种情况,可分别求得t的值;
(3)过Q作QH⊥OA于H,得到△AQH∽△ABO,进而得到QH,在利用三角形面积公式即可得到结论.
试题解析:(1)点A的坐标为(0,3);点B的坐标为(4,0).
(2)在Rt△AOB中,OA=3,OB=4,∴AB=5.
∴AP=t,QB=2t,AQ=5-2t.
△APQ与△AOB相似,可能有两种情况:
①若△APQ∽△AOB,则有![]() ,即
,即![]() , 解得
, 解得![]() .
.
②若△APQ∽△ABO,则有![]() ,即
,即![]() , 解得
, 解得![]() .
.
故t=![]() 或
或![]()
(3)过Q作QH⊥OA于H,则△AQH∽△ABO,∴AQ:AB=HQ:OB,∴(5-2t):5=QH:4,∴QH=![]() ,∴S=
,∴S=![]() APHQ
APHQ![]() ,∴
,∴ ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形的一个底角为30°,则它的顶角等于( )
A. 30°B. 40°C. 75°D. 120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】商店将某种商品按进货价提高100%后,又以八折售出,售价为80元,则这种商品的进价是( )
A. 100元B. 80元C. 60元D. 50元
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,易证△ABP∽△PCD,从而得到BPPC=ABCD(不需证明)

探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,结论BPPC=ABCD仍成立吗?请说明理由?
拓展:如图③,在△ABC中,点P是BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=4
 ,CE=3,则DE的长为 .
,CE=3,则DE的长为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y1=x+3,y2=2-x , 当x=时,y1比y2大5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,-2).
(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1 ,使它与△OAB的相似比为2:1,并分别写出点A、B的对应点A1、B1的坐标.
(2)画出将△OAB向左平移2个单位,再向上平移1个单位后的△O2A2B2 ,并写出点A、B的对应点A2、B2的坐标.
(3)判断△OA1B1与△O2A2B2 ,能否是关于某一点M为位似中心的位似图形,若是,请在图中标出位似中心M,并写出点M的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】只用下列一种正多边形就能铺满地面的是( )
A. 正十边形B. 正八边形C. 正六边形D. 正五边形
相关试题

