【题目】我国古籍《周髀算经》中早有记载“勾三股四弦五”,下面我们来探究两类特殊的勾股数.通过观察完成下面两个表格中的空格(以下a、b、c为Rt△ABC的三边,且a<b<c):
表一 表二
a | b | c | a | b | c | |
3 | 4 | 5 | 6 | 8 | 10 | |
5 | 12 | 13 | 8 | 15 | 17 | |
7 | 24 | 25 | 10 | 24 | 26 | |
9 | 41 | 12 | 37 |
(1)仔细观察,表一中a为大于1的奇数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(2)仔细观察,表二中a为大于4的偶数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(3)我们还发现,表一中的三边长“3,4,5”与表二中的“6,8,10”成倍数关系,表一中的“5,12,13”与表二中的“10,24,26”恰好也成倍数关系……请直接利用这一规律计算:在Rt△ABC中,当![]() ,
,![]() 时,斜边c的值.
时,斜边c的值.
参考答案:
【答案】 b+1=c a2=b+c b+2=c a2=2(b+c)
【解析】分析:(1)根据图表中数据结合勾股定理得出即可;
(2)利用图表中数据即可得出b、c的数量关系;
(3)利用图表中数据即可得出b、a的数量关系;
(4)利用勾股定理得出即可.
详解:(1)如图所示:
表一 表二
a | b | c | a | b | c | |
3 | 4 | 5 | 6 | 8 | 10 | |
5 | 12 | 13 | 8 | 15 | 17 | |
7 | 24 | 25 | 10 | 24 | 26 | |
9 | 40 | 41 | 12 | 35 | 37 |
(2)根据表格数据可得:
表一中a为大于l的奇数,此时b、c的数量关系是b+1=c;a、b、c之间的数量关系是a2=b+c
表二中a为大于4的偶数,此时b、c的数量关系是b+2=c;a、b、c之间的数量关系是a2=2(b+c)
(3)∵![]() ,∴
,∴![]() ,∴c=1.
,∴c=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,BE⊥AC,DF⊥AC,垂足分别为E,F,BE=DF,AE=CF.

(1)求证:△AFD≌△CEB;
(2)若∠CBE=∠BAC,四边形ABCD是怎样的四边形?证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富少年儿童的业余生活,某社区要在如图中的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B.已知AB=2.5km,CA=1.5km,DB=1.Okm,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于O,OE⊥AB,OF⊥CD。
(1)图中与∠COE互补的角是___________________; (把符合条件的角都写出来)
(2)如果∠AOC =
 ∠EOF ,求∠AOC的度数。
∠EOF ,求∠AOC的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和35°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度. (结果保留整数,参考数据:sin35°≈
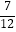 ,cos35°≈
,cos35°≈  ,tan35°≈
,tan35°≈ 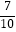 ,
, 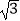 ≈1.7)
≈1.7)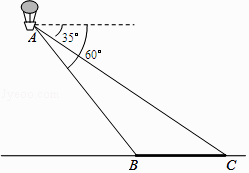
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
(1)求证:△OAE≌△OBG.
(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形
 ,使
,使 ,连接
,连接 ,再以
,再以 为边作第三个菱形
为边作第三个菱形 ,使
,使 ;…,按此规律所作的第六个菱形的边长为( )
;…,按此规律所作的第六个菱形的边长为( )
A. 9 B.
 C. 27 D.
C. 27 D. 
相关试题

