【题目】如图,在四边形ABCD中,BE⊥AC,DF⊥AC,垂足分别为E,F,BE=DF,AE=CF. 
(1)求证:△AFD≌△CEB;
(2)若∠CBE=∠BAC,四边形ABCD是怎样的四边形?证明你的结论.
参考答案:
【答案】
(1)证明:∵BE⊥AC,DF⊥AC,
∴∠AFD=∠CEB=90°.
∵AE=FC,
∴AE+EF=FC+EF,
∴AF=CE,
又∵BE=DF,
∴△AFD≌△CEB;
(2)证明:四边形ABCD为矩形.
∵△AFD≌△CEB,
∴AD=BC,∠BCE=∠DAF.
∴AD∥BC,
∴四边形ABCD为平行四边形,
∵∠CBE=∠BAC,
又∵∠CBE+∠ACB=90°,
∴∠BAC+∠ACB=90°,
∴∠ABC=90°,
∴四边形ABCD为矩形.
【解析】(1)求出AF=CE,再利用“边角边”证明即可;(2)根据全等三角形对应边相等可得AD=BC,全等三角形对应角相等可得∠BCE=∠DAF,再根据内错角相等,两直线平行证明AD∥BC,然后判断出四边形ABCD是平行四边形,求出∠ABC=90°,最后根据有一个角是直角的平行四边形是矩形证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,以大于
 BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,得四边形ABEF.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,得四边形ABEF. 求证:四边形ABEF是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】由大小相同(棱长为1分米)的小立方块搭成的几何体如下图.


(1)请在右图的方格中画出该几何体的俯视图和左视图;
(2)图中有 块小正方体,它的表面积(含下底面)为 ;
(3)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要_______个小立方块,最多要_______个小立方块.
-
科目: 来源: 题型:
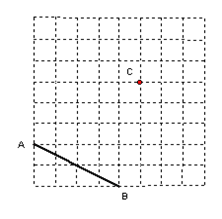
查看答案和解析>>【题目】如图,在每个小正方形的边长都为1的方格纸上有线段AB和点C.
(1)画线段BC、画射线AC.
(2)过点C画直线AB的平行线EF.
(3)过点C画直线AB的垂线,垂足为点D.
(4)求△ABC的面积是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富少年儿童的业余生活,某社区要在如图中的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B.已知AB=2.5km,CA=1.5km,DB=1.Okm,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于O,OE⊥AB,OF⊥CD。
(1)图中与∠COE互补的角是___________________; (把符合条件的角都写出来)
(2)如果∠AOC =
 ∠EOF ,求∠AOC的度数。
∠EOF ,求∠AOC的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古籍《周髀算经》中早有记载“勾三股四弦五”,下面我们来探究两类特殊的勾股数.通过观察完成下面两个表格中的空格(以下a、b、c为Rt△ABC的三边,且a<b<c):
表一 表二
a
b
c
a
b
c
3
4
5
6
8
10
5
12
13
8
15
17
7
24
25
10
24
26
9
41
12
37
(1)仔细观察,表一中a为大于1的奇数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(2)仔细观察,表二中a为大于4的偶数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(3)我们还发现,表一中的三边长“3,4,5”与表二中的“6,8,10”成倍数关系,表一中的“5,12,13”与表二中的“10,24,26”恰好也成倍数关系……请直接利用这一规律计算:在Rt△ABC中,当
 ,
, 时,斜边c的值.
时,斜边c的值.
相关试题

