【题目】如图,抛物线![]() (
(![]() )的对称轴为直线
)的对称轴为直线![]() ,与
,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,其部分图象如图所示,下列结论:①
,其部分图象如图所示,下列结论:①![]() ;②方程
;②方程![]() 的两个根是
的两个根是![]() ,
,![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;⑤当
;⑤当![]() 时,
时,![]() 随
随![]() 增大而增大.其中结论正确的个数是( )
增大而增大.其中结论正确的个数是( )

A. 5个 B. 4个 C. 3个 D. 2个
参考答案:
【答案】C
【解析】
利用抛物线与x轴的交点个数可对①进行判断;利用抛物线的对称性得到抛物线与x轴的一个交点坐标为(3, 0),则可对②进行判断;由对称轴方程得到b=-2a 然后根据x=-1时函数值为0可得到3a+c=0,则可对③进行判断;由题知x=-1时,y=0,可判断④的正确性,根据二次函数的性质对⑤进行判断.
①由题意得:抛物线与x轴有两个交点,所以b2- 4ac> 0, 即4ac< b2,所以①正确;
②因为抛物线与x轴的一个交点为(- 1,0),抛物线的对称轴为x= 1,所以另一个交点为(3, 0),所以x1=-1,x2 =3是方程ax2 +bx+c= 0的解,所以②正确;
③因为对称轴为x= 1,所以有![]() =1,即a=-2b,将(- 1,0)代入抛物线得: 3a+c=0, 所以③不正确;
=1,即a=-2b,将(- 1,0)代入抛物线得: 3a+c=0, 所以③不正确;
④由题知,x=-1时,y=0, 所以④不正确;
⑤当x< 0时,函数图象在x= 1左侧,所以此时y随x增大而增大,所以⑤正确。综上:①②⑤正确,故答案选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
(1)当t=2时,则AP= ,此时点P的坐标是 。
(2)当t=3时,求过点P的直线l:y=-x+b的解析式?
(3)当直线l:y=-x+b从经过点M到点N时,求此时点P向上移动多少秒?
(4)点Q在x轴时,若S△ONQ=8时,请直按写出点Q的坐标是 。

-
科目: 来源: 题型:
查看答案和解析>>【题目】材料阅读:
若a是正整数,则长度为
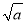 的线段是有可能表示正方形网格中两个格点之间的距离(设小正方形的长度为单位1).如图1所示,A、B两点之间的距离就是
的线段是有可能表示正方形网格中两个格点之间的距离(设小正方形的长度为单位1).如图1所示,A、B两点之间的距离就是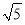 .
.
(1)在图1中以A为一个端点,画出一条长为
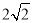 的线段AC;
的线段AC;(2)
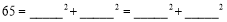 (空格处填正整数,两组数要求不一样),并根据你填的数字,在图2中画出两种对应的线段,其长度均为
(空格处填正整数,两组数要求不一样),并根据你填的数字,在图2中画出两种对应的线段,其长度均为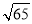 ;
;(3)利用材料所给的方法,直接写出三边长分别为
 、
、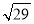 、
、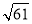 的三角形的面积:__________.
的三角形的面积:__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在同一坐标系下,一次函数
 与二次函数
与二次函数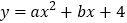 的图象大致可能是( )
的图象大致可能是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,CD=2,求EC的长.
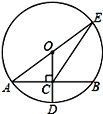
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:请你添加一个条件_____可以得到


-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示:

(1)根据图示填写下表:
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
(2)结合两队成绩的平均数中中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手的成绩较为稳定.
相关试题

