【题目】材料阅读:
若a是正整数,则长度为![]() 的线段是有可能表示正方形网格中两个格点之间的距离(设小正方形的长度为单位1).如图1所示,A、B两点之间的距离就是
的线段是有可能表示正方形网格中两个格点之间的距离(设小正方形的长度为单位1).如图1所示,A、B两点之间的距离就是![]() .
.

(1)在图1中以A为一个端点,画出一条长为![]() 的线段AC;
的线段AC;
(2)![]() (空格处填正整数,两组数要求不一样),并根据你填的数字,在图2中画出两种对应的线段,其长度均为
(空格处填正整数,两组数要求不一样),并根据你填的数字,在图2中画出两种对应的线段,其长度均为![]() ;
;
(3)利用材料所给的方法,直接写出三边长分别为![]() 、
、![]() 、
、![]() 的三角形的面积:__________.
的三角形的面积:__________.
参考答案:
【答案】(1)详见解析;(2)8、1;7、4;图形见解析;(3)6.5
【解析】
(1)由勾股定理可知![]() ,则问题可解;(2)由勾股定理可知
,则问题可解;(2)由勾股定理可知![]() 则问题可解;(3)由勾股定理可以画出相应三角形,再由割补法求面积即可.
则问题可解;(3)由勾股定理可以画出相应三角形,再由割补法求面积即可.
解:(1)如图1;
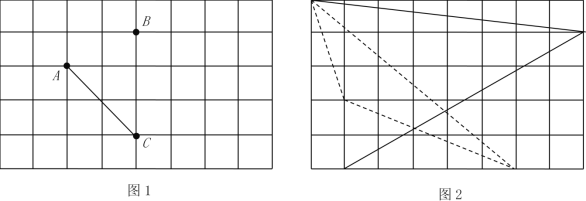
(2)由于![]()
故答案为8、1;7、4;
由此在图2中画出满足条件的线段,如图2中两条实线所示;
(3)在仿照材料中所给的方法,可构造如图2的虚线所示三角形
求三角形面积为:![]()
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:

①旋转角的度数;
②线段OD的长;
③∠BDC的度数.
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.当OA、OB、OC满足什么条件时,∠ODC=90°?请给出证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 经过点
经过点 ,
, .
.
(1)求直线
 的解析式;
的解析式;(2)若直线
 与直线
与直线 相交于点
相交于点 ,求点
,求点 的坐标;
的坐标;(3)根据图象,直接写出关于
 的不等式
的不等式 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
(1)当t=2时,则AP= ,此时点P的坐标是 。
(2)当t=3时,求过点P的直线l:y=-x+b的解析式?
(3)当直线l:y=-x+b从经过点M到点N时,求此时点P向上移动多少秒?
(4)点Q在x轴时,若S△ONQ=8时,请直按写出点Q的坐标是 。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在同一坐标系下,一次函数
 与二次函数
与二次函数 的图象大致可能是( )
的图象大致可能是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 (
( )的对称轴为直线
)的对称轴为直线 ,与
,与 轴的一个交点坐标为
轴的一个交点坐标为 ,其部分图象如图所示,下列结论:①
,其部分图象如图所示,下列结论:① ;②方程
;②方程 的两个根是
的两个根是 ,
, ;③
;③ ;④当
;④当 时,
时, 的取值范围是
的取值范围是 ;⑤当
;⑤当 时,
时, 随
随 增大而增大.其中结论正确的个数是( )
增大而增大.其中结论正确的个数是( )
A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
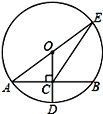
查看答案和解析>>【题目】如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,CD=2,求EC的长.
相关试题

