搜索
【题目】△ABC和△A′B′C′在平面直角坐标系中的位置分别如图所示.
（1）分别写出下列各点的坐标：A_______；B_______；C_______；
（2）△ABC由△A′B′C′经过怎样的平移得到？
答：_____________________________________
（3）求△ABC面积.
参考答案：
【答案】(1,3) (2,0) (3,1) 向右平移4个单位长度，再向上平移2个单位长度
【解析】
（1）直接利用已知图形得出各点坐标即可；
（2）利用对应点位置得出平移规律；
（3）利用△ABC所在矩形面积减去周围三角形进而得出答案．
(1)
（2）向右平移4个单位长度，再向上平移2个单位长度
（3）如图，
矩形
,
=矩形
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题引入：
（1）如图①所示，△ABC中，点O是∠ABC和∠ACB的平分线的交点，若∠A=
，则∠BOC= (用
表示)；不用说明理由，直接填空.如图②所示，
，
，若
，则∠BOC= (用
表示). 不用说明理由，直接填空.
（2）如图③所示，
，
，若，则∠BOC= (用
表示)，填空并说明理由.类比研究：
（3）BO，CO分别是△ABC的外角∠DBC，∠ECB的n等分线，
它们交于点O，
，
，若，则
(用和n表示).不用说明理由，直接填空. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，△ABC中，∠ACB=90°，AC=6cm，BC =8cm.点P从A点出发,沿
路径向终点B运动，点Q从B点出发,沿
路径向终点A运动.点P 和Q分别
和
的运动速度同时开始运动，两点都要到相应的终点时才能停止运动，在某时刻，分别过点P和Q作PE⊥l于E，QF⊥l于F.则点P运动多少秒时，△PEC和△CFQ全等？请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系
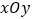中，对于点
，我们把点
叫做点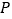
的衍生点．已知点
的衍生点为
，点的衍生点为
，点的衍生点为
这样依次得到点
若点的坐标为
，若点
在第四象限，则
范围分别为______________. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，某抛物线的对称轴为直线x=2，点E是该抛物线顶点，抛物线与y轴交于点C，过点C作CD∥x轴，与抛物线交于点B，与对称轴交于点D，点A是对称轴上一点，连结AC，AB，若△ABC是等边三角形，则图中阴影部分图形的面积之和是 ．
-
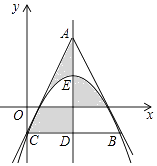
科目： 来源： 题型：
查看答案和解析>>【题目】某学校的复印任务原来由甲复印社承接，其收费y（元）与复印页数x（页）的关系如下表：
x（页）
100
200
400
1000
…
y（元）
40
80
160
400
（1）若y与x满足初中学过的某一函数关系，求函数的解析式;
（2）现在乙复印社表示：若学校先按每月付给200元的承包费，则可按每页0.15元收费，则乙复印社每月收费y（元）与复印页数x（页）的函数关系为________________，
（3）学校准备复印材料1000页，应选择哪个复印社比较优惠？
-
科目： 来源： 题型：
查看答案和解析>>【题目】材料理解：如图1点P,Q是标准体育场400m跑道上两点，沿跑道从P到Q既可以逆时针，也可以顺时针，我们把沿跑道从点P到点Q的顺时针路程与逆时针路程的较小者叫P、Q两点的最佳环距离.(如图1，PQ顺时针的路程为120m,逆时针的路程为280m,则PQ的最佳环距离为120m).
问题提出：一次校运动800m预决赛中，如图2有甲、乙两名运动员他们同时同地从点M处出发，匀速跑步，他们之间的最佳环距离y(m)与乙用的时间x(s)之间的函数关系如图所示；解决以下问题：
（1）a=_________,乙的速度为___________.
（2）求线段BC的解析式，并写出自变量的范围.
（3）若本次运动会是1000m预决赛，甲完成比赛后是否有可能比乙多跑一圈，计算说明.
相关试题
