【题目】阅读材料,解答相应的问题:
如果一个正整数能表示为两个正整数的平方差,那么称这个正整数为“智慧数”,否则,称这个正整数为“非慧数”。
例如:![]() …
…
因此:3,5,8,……都是“智慧数”;而1,2,4……都是“非智慧数”。
对于“智慧数”,有如下结论:
①设![]() 为正整数(
为正整数(![]() ),则
),则![]() ,∴除1以外,所有的奇数都是“智慧数”;
,∴除1以外,所有的奇数都是“智慧数”;
②设![]() 为正整数(
为正整数(![]() ),则
),则![]() = ,∴
= ,∴
都是“智慧数”;
(1)补全材料中空缺的部分;
(2)求出所有大于5而小于20的“非智慧数”;
参考答案:
【答案】(1)![]() ;(2)
;(2)
【解析】分析:(1)根据平方差公式即可求出答案.
(2)由(1)得奇数和4的倍数是智慧数,故可得解.
详解:(1)![]() ,奇数,4的倍数;
,奇数,4的倍数;
(2)除去奇数:7,9,11,13,15,17,19,除去4的正整数倍数8,12,16,
则“非智慧数”有6,10,14,18
-
科目: 来源: 题型:
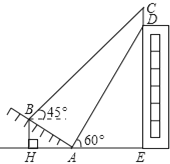
查看答案和解析>>【题目】如图,我市某中学在创建“特色校园”的活动中,将学校的办学理念做成了宣传牌(CD),放置在教学楼的顶部(如图所示),该中学数学活动小组的同学在山坡坡脚A处测得宣传牌底D的仰角为60°,沿坡AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为
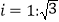 ,AB=10米,AE=15米.
,AB=10米,AE=15米.(1)求点B距水平面AE的高度BH;
(2)求宣传牌CD的高度.(结果精确到0.1米.参考数据:
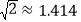 ,
,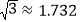 )
)
-
科目: 来源: 题型:
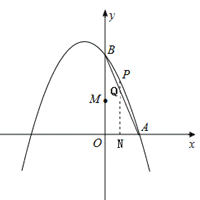
查看答案和解析>>【题目】如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是直线x=﹣1.
(1)求抛物线对应的函数关系式;
(2)点N在线段OA上,点M在线段OB上,且OM=2ON,过点N作x轴的垂线交线段AB于点Q,交抛物线于点P.
①当ON为何值时,四边形OMPN为矩形;
②△AOQ能否为等腰三角形?若能,求出此时ON的值;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD 中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N ,连接OM,ON,MN .下列五个结论:①△CNB≌△DMC ;②△CON≌△DOM ;③△OMN≌△OAD ;④
 ;⑤若AB=2,则
;⑤若AB=2,则 的最小值是
的最小值是 ,其中正确结论的个数是 ( )
,其中正确结论的个数是 ( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BI,CI分别平分∠ABC,∠ACB,过I点作DE∥BC,交AB于D,交AC于E,给出下列结论:①△DBI是等腰三角形;②△ACI是等腰三角形;③AI平分∠BAC;④△ADE周长等于AB+AC.其中正确的是( )

A. ①②③ B. ②③④ C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
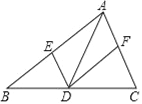
A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学老师布置了一道思考题“计算:(-
 )÷(
)÷(
 )”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
)”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.小明的解法:原式的倒数为(

 )÷(
)÷( )=(
)=(
 )×(-12)=-4+10=6,所以(-
)×(-12)=-4+10=6,所以(- )÷(
)÷(
 )=
)= .
.(1)请你判断小明的解答是否正确,并说明理由.
(2)请你运用小明的解法解答下面的问题.
计算:(-
 )÷(
)÷(
 +
+ ).
).
相关试题

