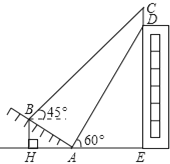
【题目】如图,我市某中学在创建“特色校园”的活动中,将学校的办学理念做成了宣传牌(CD),放置在教学楼的顶部(如图所示),该中学数学活动小组的同学在山坡坡脚A处测得宣传牌底D的仰角为60°,沿坡AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为![]() ,AB=10米,AE=15米.
,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求宣传牌CD的高度.(结果精确到0.1米.参考数据:![]() ,
,![]() )
)
参考答案:
【答案】(1)BH=5 (2)2.7
【解析】分析:(1)在Rt△ABH中,由tan∠BAH=![]() .得到∠BAH=30°,于是得到结果BH=AB.sin∠BAH=10.sin30°=10×
.得到∠BAH=30°,于是得到结果BH=AB.sin∠BAH=10.sin30°=10×![]() =5;
=5;
(2)在Rt△ABH中,AH=AB.cos∠BAH=10.cos30°=5![]() ,在Rt△ADE中,tan∠DAE=
,在Rt△ADE中,tan∠DAE=![]() ,即tan60°=
,即tan60°=![]() ,得到DE=15
,得到DE=15![]() ,如图,过点B作BF⊥CE,垂足为F,求出BF=AH+AE=5
,如图,过点B作BF⊥CE,垂足为F,求出BF=AH+AE=5![]() +15,于是得到DF=DE-EF=DE-BH=15
+15,于是得到DF=DE-EF=DE-BH=15![]() -5,在Rt△BCF中,∠C=90°-∠CBF=90°-45°=45°,求得∠C=∠CBF=45°,得出CF=BF=5
-5,在Rt△BCF中,∠C=90°-∠CBF=90°-45°=45°,求得∠C=∠CBF=45°,得出CF=BF=5![]() +15,即可求得结果.
+15,即可求得结果.
详解:(1)在Rt△ABH中,
∵tan∠BAH=![]() .
.
∴∠BAH=30°,
∴BH=AB.sin∠BAH=10.sin30°=10×![]() =5.
=5.
答:点B距水平面AE的高度BH是5米;
(2)在Rt△ABH中,AH=AB.cos∠BAH=10.cos30°=5![]() ,
,
在Rt△ADE中,tan∠DAE=![]() ,
,
即tan60°=![]() ,∴DE=15
,∴DE=15![]() ,
,
如图,过点B作BF⊥CE,垂足为F,
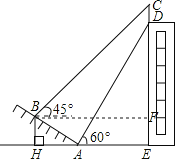
∴BF=AH+AE=5![]() +15,
+15,
DF=DE-EF=DE-BH=15![]() -5,
-5,
在Rt△BCF中,∠C=90°-∠CBF=90°-45°=45°,
∴∠C=∠CBF=45°,
∴CF=BF=5![]() +15,
+15,
∴CD=CF-DF=5![]() +15-(15
+15-(15![]() -5)=20-10
-5)=20-10![]() ≈20-10×1.732≈2.7(米),
≈20-10×1.732≈2.7(米),
答:广告牌CD的高度约为2.7米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动:擦出智慧的火花---------由特殊到一般的数学思想.
数学课上,李老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC上的点,过点E作EF⊥AE,过点F作FG⊥BC交BC的延长线于点G..
(1)求证:∠BAE=∠FEG.
(2)同学们很快做出了解答,之后李老师将题目修改成:如图2,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线于点F,求证:AE=EF.
经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.请借助图1完成小明的证明;
在(2)的基础上,同学们作了进一步的研究:
(3)小聪提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小聪的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形BFEC中,连接FC,并延长至点D,延长CF至点A,使DC=AF,连接AB、DE.
(1)求证:AB∥DE.
(2)若平行四边形BFEC是菱形,且∠ABC=90°,AB=4,BC=3,则CF= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:
①0是最小的整数;
②有理数不是正数就是负数;
③正整数、负整数、正分数、负分数统称为有理数;
④非负数就是正数;
⑤
 不仅是有理数,而且是分数;
不仅是有理数,而且是分数;⑥
 是无限不循环小数,所以不是有理数;
是无限不循环小数,所以不是有理数;⑦无限小数不都是有理数;
⑧正数中没有最小的数,负数中没有最大的数.
其中错误的说法的个数为( )
A.7个B.6个C.5个D.4个
-
科目: 来源: 题型:
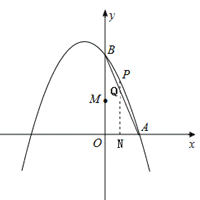
查看答案和解析>>【题目】如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是直线x=﹣1.
(1)求抛物线对应的函数关系式;
(2)点N在线段OA上,点M在线段OB上,且OM=2ON,过点N作x轴的垂线交线段AB于点Q,交抛物线于点P.
①当ON为何值时,四边形OMPN为矩形;
②△AOQ能否为等腰三角形?若能,求出此时ON的值;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD 中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N ,连接OM,ON,MN .下列五个结论:①△CNB≌△DMC ;②△CON≌△DOM ;③△OMN≌△OAD ;④
 ;⑤若AB=2,则
;⑤若AB=2,则 的最小值是
的最小值是 ,其中正确结论的个数是 ( )
,其中正确结论的个数是 ( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,解答相应的问题:
如果一个正整数能表示为两个正整数的平方差,那么称这个正整数为“智慧数”,否则,称这个正整数为“非慧数”。
例如:
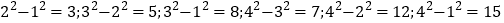 …
…因此:3,5,8,……都是“智慧数”;而1,2,4……都是“非智慧数”。
对于“智慧数”,有如下结论:
①设
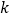 为正整数(
为正整数(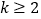 ),则
),则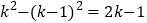 ,∴除1以外,所有的奇数都是“智慧数”;
,∴除1以外,所有的奇数都是“智慧数”;②设
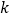 为正整数(
为正整数( ),则
),则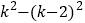 = ,∴
= ,∴ 都是“智慧数”;
(1)补全材料中空缺的部分;
(2)求出所有大于5而小于20的“非智慧数”;
相关试题

