【题目】在平面直角坐标系中,点![]() 是坐标原点,四边形
是坐标原点,四边形![]() 是菱形,点
是菱形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的负半轴上,直线
轴的负半轴上,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 边交
边交![]() 轴于点
轴于点![]() .
.
(1)如图1,求直线![]() 的解析式;
的解析式;

(2)如图2,连接![]() ,动点
,动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 方向以1个单位/秒的速度向终点
方向以1个单位/秒的速度向终点![]() 匀速运动,设
匀速运动,设![]() 的面积为
的面积为![]() (
(![]() ),点
),点![]() 的运动时间为
的运动时间为![]() 秒,求
秒,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围.
的取值范围.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() (
(![]() )
)
【解析】
(1)先利用点A的坐标和勾股定理求出OA的长度,然后利用菱形的性质可求出点C的坐标,最后利用待定系数法即可求出直线AC的解析式;
(2)先利用菱形的性质证明![]() ,则有
,则有![]() 然后根据直线AC的解析式求出点D的坐标,最后利用三角形的面积公式
然后根据直线AC的解析式求出点D的坐标,最后利用三角形的面积公式![]() 求解即可.
求解即可.
(1)过点A作![]() 轴于点M,
轴于点M,

∵点![]() 的坐标为
的坐标为![]() ,
,
∴![]() .
.
∵![]() 轴,
轴,
∴![]() ,
,
∴![]() .
.
∵四边形OABC是菱形,
∴![]() ,
,
∴![]() .
.
设直线AC的解析式为![]() ,
,
将![]() 代入解析式中得
代入解析式中得
![]() 解得
解得![]()
∴直线AC解析式为![]() ;
;
(2)如图,

∵四边形OABC是菱形,
∴![]() ,
,
![]() ,
,
![]() .
.
∵直线AC解析式为![]() ,
,
令![]() ,则
,则![]() ,
,
∴![]() ,
,
![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:

根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲

7
7
1.2
乙
7

8
4.2
(1)写出表格中
 ,
, 的值;
的值;(2)从方差的角度看,若选派其中一名参赛,你认为应选哪名队员?并说明理.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, 是
是 上一点,
上一点, 垂直平分
垂直平分 ,分别交
,分别交 ,
, ,
, 于点
于点 ,
, ,
, ,连接
,连接 ,
, .
.(1)求证:四边形
 是菱形;
是菱形;(2)若
 ,
, 为
为 的中点,
的中点, ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),抛物线W1:y=﹣x2+4x与x轴的正半轴交于点B,顶点为A,抛物线W2与W1关于x轴对称,顶点为D.
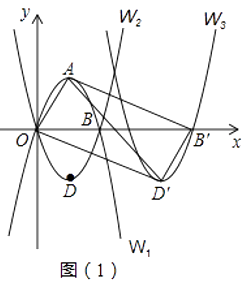
(1)求抛物线W2的解析式;
(2)将抛物线W2向右平移m个单位,点D的对应点为D′,点B的对应点为B′,则当m为何值时,四边形AOD′B′为矩形?请直接写出m的值.
(3)在(2)的条件下,将△AOD′沿x轴的正方向向右平移n个单位(0<n<5),得到△A′O′D′′,AD′分别与O′A′、O′D′′交于点M、点P,A′D′′分别与AB′、B′D′交于点N、点Q.
①求当n为何值时,四边形MNQP为菱形?
②若四边形MNQP的面积为S,求S关于n的函数关系式;并求当n为何值时,S的值最大?最大值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为
 ,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB的延长线于点F,则EF的长为( )
,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB的延长线于点F,则EF的长为( )
A.2
B.4
C.2
D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB,∠CAB=40°,连接BD,OD,则∠AOD+∠ABD的度数为( )

A.100°
B.110°
C.120°
D.150° -
科目: 来源: 题型:
查看答案和解析>>【题目】某造纸企业为了更好地处理污水问题,决定购买10台新型污水处理设备.甲、乙两种型号的设备可选,其中每台的价格,月处理污水量如表:
A型
B型
价格(万元/)
10
8
处理污水量(吨/月)
180
150
(1)经预算:该企业购买污水处理设备的资金不超过85万元,你认为该企业有哪几种购买方案.
(2)在(1)的条件下,若每月需要处理的污水不低于1530吨,为了节约资金,请你为该企业设计一种最省钱的购买方案.
相关试题

