搜索
【题目】如图，AB是⊙O的直径，弦CD⊥AB，∠CAB=40°，连接BD，OD，则∠AOD+∠ABD的度数为（ ）
A.100°
B.110°
C.120°
D.150°
参考答案：
【答案】D
【解析】解：∵∠CAB=40°，
∴∠BDC=40°．
∵CD⊥AB，
∴∠ABD=90°﹣40°=50°，
∴∠AOD=2∠ABD=100°，
∴∠AOD+∠ABD=100°+50°=150°．
所以答案是：D．
【考点精析】根据题目的已知条件，利用垂径定理和圆周角定理的相关知识可以得到问题的答案，需要掌握垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图（1），抛物线W1：y=﹣x2+4x与x轴的正半轴交于点B，顶点为A，抛物线W2与W1关于x轴对称，顶点为D．
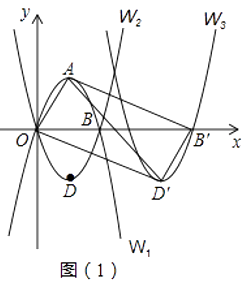
（1）求抛物线W2的解析式；
（2）将抛物线W2向右平移m个单位，点D的对应点为D′，点B的对应点为B′，则当m为何值时，四边形AOD′B′为矩形？请直接写出m的值．
（3）在（2）的条件下，将△AOD′沿x轴的正方向向右平移n个单位（0＜n＜5），得到△A′O′D′′，AD′分别与O′A′、O′D′′交于点M、点P，A′D′′分别与AB′、B′D′交于点N、点Q．
①求当n为何值时，四边形MNQP为菱形？
②若四边形MNQP的面积为S，求S关于n的函数关系式；并求当n为何值时，S的值最大？最大值为多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，点
是坐标原点，四边形
是菱形，点
的坐标为
，点
在
轴的负半轴上，直线
交
轴于点
，
边交轴于点
．（1）如图1，求直线
的解析式；
（2）如图2，连接
，动点
从点出发，沿线段
方向以1个单位/秒的速度向终点
匀速运动，设
的面积为
（
），点的运动时间为
秒，求与之间的函数关系式，并直接写出自变量的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的边长为
，连接AC，AE平分∠CAD，交BC的延长线于点E，FA⊥AE，交CB的延长线于点F，则EF的长为（ ）
A.2
B.4
C.2
D.4 -
科目： 来源： 题型：
查看答案和解析>>【题目】某造纸企业为了更好地处理污水问题，决定购买10台新型污水处理设备．甲、乙两种型号的设备可选，其中每台的价格，月处理污水量如表：
A型
B型
价格（万元/）
10
8
处理污水量（吨/月）
180
150
（1）经预算：该企业购买污水处理设备的资金不超过85万元，你认为该企业有哪几种购买方案．
（2）在（1）的条件下，若每月需要处理的污水不低于1530吨，为了节约资金，请你为该企业设计一种最省钱的购买方案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在正方形ABCD中，对角线AC、BD交于点O，点P在线段BC上（不含点B），∠BPE＝
∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．（1）当点P与点C重合时（如图①）：
①求证：△BOG≌△POE；②猜想：
＝ ；（2）当点P与点C不重合时，如图②，
的值会改变吗？试说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市南县大力发展农村旅游事业，全力打造“洞庭之心湿地公园”，其中罗文村的“花海、涂鸦、美食”特色游享誉三湘，游人如织．去年村民罗南洲抓住机遇，返乡创业，投入20万元创办农家乐（餐饮＋住宿），一年时间就收回投资的80%，其中餐饮利润是住宿利润的2倍还多1万元．
（1）求去年该农家乐餐饮和住宿的利润各为多少万元？
（2）今年罗南洲把去年的餐饮利润全部用于继续投资，增设了土特产的实体店销售和网上销售项目．他在接受记者采访时说：“我预计今年餐饮和住宿的利润比去年会有10%的增长，加上土特产销售的利润，到年底除收回所有投资外，还将获得不少于10万元的纯利润．”请问今年土特产销售至少有多少万元的利润？
相关试题
