【题目】如图(1),抛物线W1:y=﹣x2+4x与x轴的正半轴交于点B,顶点为A,抛物线W2与W1关于x轴对称,顶点为D.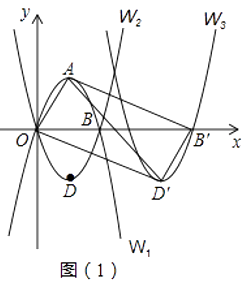
(1)求抛物线W2的解析式;
(2)将抛物线W2向右平移m个单位,点D的对应点为D′,点B的对应点为B′,则当m为何值时,四边形AOD′B′为矩形?请直接写出m的值.
(3)在(2)的条件下,将△AOD′沿x轴的正方向向右平移n个单位(0<n<5),得到△A′O′D′′,AD′分别与O′A′、O′D′′交于点M、点P,A′D′′分别与AB′、B′D′交于点N、点Q.
①求当n为何值时,四边形MNQP为菱形?
②若四边形MNQP的面积为S,求S关于n的函数关系式;并求当n为何值时,S的值最大?最大值为多少?
参考答案:
【答案】
(1)解:由y=﹣x2+4x=﹣(x﹣2)2+4得,点A坐标为(2,4),
∵抛物线W2与W1关于x轴对称,
∴点D坐标为(2,﹣4),
∴抛物线W2的解析式为y=(x﹣2)2﹣4,即y=x2﹣4x
(2)解:∵点A坐标为(2,4),
∴直线OA=2x,
∵点D坐标为(2,﹣4),
∴D′(2+m,﹣4),
∴直线OD′的解析式为y=﹣ ![]() x,
x,
∵四边形AOD′B′为矩形,
∴AO⊥OD′,
∴2×(﹣ ![]() )=﹣1,
)=﹣1,
∴m=6,
∴当m的值为6时,四边形AOD′B′为矩形
(3)解:①当y=0时,﹣x2+4x=0,解得x1=0,x2=4.
∴点B坐标为(4,0),
又∵m=6,
∴B′坐标为(10,0),
∴OB′=10;
设矩形AOD′B′的对角线AD′与OB′交于点E,A′D′′与x轴交于点F..
∵四边形AOD′B′为矩形,
∴AE=OE=B′E=D′E=5,
∴∠OAE=∠AOE,∠EOD′=∠DOE.
∵A′O′∥AO,O′D′′∥OD′,
∴∠EMO′=∠MO′E,∠EO′P=∠EPO′,
∴ME=EO′=EP,
∵OE=5,OO′=n,
∴O′E=5﹣n,
∴ME=EP=5﹣n.
同理NF=FQ=FB′=5﹣n.
∵MP∥NQ,
∴四边形MEFN,EPQF为平行四边形.
∴MN∥EF∥PQ,
∴四边形MNQP为平行四边形,
∴当MN=MP时,四边形MNQP为菱形.
∵MN=AA′=n,MP=2O′E=10﹣2n.
∴n=10﹣2n.
解得n= ![]() .
.
∴当n= ![]() 时,四边形MNQP为菱形;
时,四边形MNQP为菱形;
②过M作MH⊥x轴,垂足为H,过A作AG⊥x轴,垂足为G,

则△MHE∽△AGE,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴MH= ![]() (5﹣n),
(5﹣n),
∴S=2S□MEFN=2× ![]() (5﹣n)﹣n=﹣
(5﹣n)﹣n=﹣ ![]() n2+8n,
n2+8n,
∵S=﹣ ![]() (n﹣
(n﹣ ![]() )2+10,∵﹣
)2+10,∵﹣ ![]() <0,
<0,
∴当n= ![]() 时,S的值最大,最大值为10.
时,S的值最大,最大值为10.
【解析】(1)抛物线关于x 轴对称与点的对称类似,横坐标不变,纵坐标变为其相反数,即-y=﹣x2+4x,y=x2-4x;(2)先求OA解析式,再用m的代数式表示直线OD′的解析式,根据矩形的性质,得出二直线互相垂直,即斜率之积为-1,求出m;(3)由已知可得四边形MNQP为平行四边形,若四边形MNQP为菱形须MN=MP,构建n的方程n=10﹣2n,求出n;最值问题可运用函数思想,构建S关于n的函数,二次函数可配成顶点式,求出最值.
-
科目: 来源: 题型:
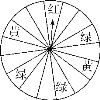
查看答案和解析>>【题目】端午节期间,某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准红色、黄色或绿色区域,顾客就可以分别获得玩具熊、童话书、水彩笔.小明和妈妈购买了125元的商品,请你回答下列问题:
(1)小明获得奖品的概率是多少?
(2)小明获得玩具熊、童话书、水彩笔的概率分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:

根据以上信息,整理分析数据如下:
平均成绩/环
中位数/环
众数/环
方差
甲

7
7
1.2
乙
7

8
4.2
(1)写出表格中
 ,
, 的值;
的值;(2)从方差的角度看,若选派其中一名参赛,你认为应选哪名队员?并说明理.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, 是
是 上一点,
上一点, 垂直平分
垂直平分 ,分别交
,分别交 ,
, ,
, 于点
于点 ,
, ,
, ,连接
,连接 ,
, .
.(1)求证:四边形
 是菱形;
是菱形;(2)若
 ,
, 为
为 的中点,
的中点, ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
 是坐标原点,四边形
是坐标原点,四边形 是菱形,点
是菱形,点 的坐标为
的坐标为 ,点
,点 在
在 轴的负半轴上,直线
轴的负半轴上,直线 交
交 轴于点
轴于点 ,
, 边交
边交 轴于点
轴于点 .
.(1)如图1,求直线
 的解析式;
的解析式;
(2)如图2,连接
 ,动点
,动点 从点
从点 出发,沿线段
出发,沿线段 方向以1个单位/秒的速度向终点
方向以1个单位/秒的速度向终点 匀速运动,设
匀速运动,设 的面积为
的面积为 (
( ),点
),点 的运动时间为
的运动时间为 秒,求
秒,求 与
与 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量 的取值范围.
的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为
 ,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB的延长线于点F,则EF的长为( )
,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB的延长线于点F,则EF的长为( )
A.2
B.4
C.2
D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB,∠CAB=40°,连接BD,OD,则∠AOD+∠ABD的度数为( )

A.100°
B.110°
C.120°
D.150°
相关试题

