【题目】如图,已知A,B分别为数轴上的两点,点A表示的数是﹣30,点B表示的数是50.
![]()
(1)请写出线段AB中点M表示的数是 .
(2)现有一只蚂蚁P从点B出发,以每秒3个单位长度的速度沿数轴向左移动,同时另一只蚂蚁Q恰好从点A出发,以每秒2个单位长度的速度沿数轴向右移动,设两只蚂蚁在数轴上的点C相遇.
①求A、B两点间的距离;
②求两只蚂蚁在数轴上的点C相遇时所用的时间;
③求点C对应的数是多少?
(3)若蚂蚁P从点B出发,以每秒3个单位长度的速度沿数轴向左运动,同时另一只蚂蚁恰好从A点出发,以每秒2个单位长度的速度沿数轴也向左运动,设两只蚂蚁在数轴上的D点相遇,求D点表示的数是多少?
参考答案:
【答案】(1)10;(2)①80;②16秒;③2;(3)-190.
【解析】
首先计算出AB长度,再根据中点平分线段可得点M表示的数;
①A、B间的距离用两点表示的数进行加减运算即可得;
②用路程除以速度即可表示时间;
③用50减去蚂蚁P的爬行路程即可得;
(3)设两只蚂蚁t秒后相遇,由题意得:定在A点左侧相遇,根据等量关系列出方程,然后可计算出运动时间,再根据A点表示的数,进而可得D点对应的数.
解:(1)AB=50+(﹣30)=20
∴AB中点M表示的数是10.
故答案为:10
(2)①A、B两点间的距离为:50﹣(﹣30)=80
②两只蚂蚁在数轴上的点C相遇时所用的时间为:80÷(3+2)=16(秒)
③点C对应的数是:50﹣16×3=2
(3)设两只蚂蚁t秒后相遇,可得: 2t+80=3t
解得 t=80
故 D点表示的数是:-( ![]() )-30=﹣190.
)-30=﹣190.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家电销售商场电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商场用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)现在商场准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13200元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
,  ,
,  ,试说明:BE∥CF.
,试说明:BE∥CF.完善下面的解答过程,并填写理由或数学式:
解:∵
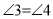 (已知)
(已知)∴AE∥ ( )
∴
 ( )
( )∵
 (已知)
(已知)∴
 ( )
( )∴DC∥AB( )
∴
 ( )
( )即

∵
 (已知)
(已知)∴
 ( )
( )即

∴BE∥CF( ) .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
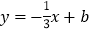 与x轴交于点A,与y轴交于点B,与直线y=x交于点E,点E的横坐标为3
与x轴交于点A,与y轴交于点B,与直线y=x交于点E,点E的横坐标为3(1) 求点A的坐标
(2) 在x轴上有一点P(m,0),过点P作x轴的垂线,与直线
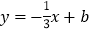 交于点C,与直线y=x 交于点D.若CD≥4,则m的取值范围为___________________
交于点C,与直线y=x 交于点D.若CD≥4,则m的取值范围为___________________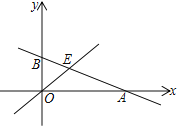
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上一点,OD平分∠AOC.
(1)若∠AOC=60°,请求出∠AOD和∠BOC的度数.
(2)若∠AOD和∠DOE互余,且∠AOD=
 ∠AOE,请求出∠AOD和∠COE的度数.
∠AOE,请求出∠AOD和∠COE的度数.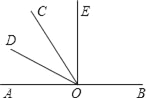
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.
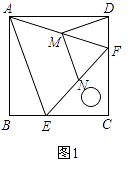
(1)尝试探究:
结论1:DM、MN的数量关系是;
结论2:DM、MN的位置关系是;
(2)猜想论证:证明你的结论.
(3)拓展:如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,(1)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.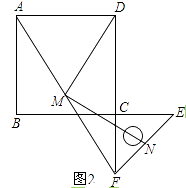
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅客携带x kg的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李重量x kg的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李重量x kg的对应关系


(1) 如果旅客选择托运,求可携带的免费行李的最大重量为多少kg?
(2) 如果旅客选择快递,当1<x≤15时,直接写出快递费y2(元)与行李的重量x kg之间的函数关系式
(3) 某旅客携带25kg的行李,设托运m kg行李(10≤m<24,m为正整数),剩下的行李选择快递.当m为何值时,总费用y的值最小?并求出其最小值是多少元?
相关试题

