【题目】数学课上,教师出示某区篮球赛积分表如下:

(1)从表中可以看出,负一场积多少分,胜一场积多少分;
(2)请你帮忙算出二队胜了多少场?
(3)在这次比赛中,一个队胜场总积分能不能等于它的负场总积分?
(4)在计算五队、六队胜出场次的时候,老师还没等同学们计算出来就立刻说出了答案,老师解释说:“我是通过找到积分与胜场之间的数量关系求出来的”,请你说出其中的奥秘.
参考答案:
【答案】(1)负1场积分2分;胜1场积3分;(2)二队胜了7场;(3)不能;(4)积分与获胜的场数之差=22.
【解析】
(1)根据三队负11场得22分,可知负1场,积2分;由一队胜10场负1场积分32分可得胜一场的积分;
(2)设二队胜x场,负(11-x)场,根据积分29分列方程,求解即可;
(3)设这次比赛一个队共胜x场,则负(11﹣x)场,然后根据得分列出方程求解即可;
(4)设这次比赛一个队共胜x场,则负(11﹣x)场,积分为y,根据y=胜场积分+负场积分=3x+2(11﹣x)=x+22,即可得到结论.
(1)三队负11场得22分,可知负1场积分=22÷11=2(分);由一队胜10场可知,其负1场,故胜1场积分=(32-1×2)÷10=3(分);
(2)设二队胜x场,负(11-x)场.根据题意得:
3x+2(11-x)=29
解得:x=7.
答:二队胜了7场.
(3)设这次比赛一个队共胜x场,则负(11﹣x)场,根据题意得:
3x=2(11-x)
解得:x=![]() .
.
∵比赛场次x是正整数,∴一个队胜场总积分不能等于它的负场总积分.
(4)设这次比赛一个队共胜x场,则负(11﹣x)场,积分为y,根据题意得:
y=3x+2(11﹣x)=x+22,∴积分与获胜的场数之差=22.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在综合与实践课上,同学们以“一个含
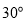 的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线
的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线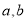 且
且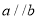 和直角三角形
和直角三角形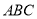 ,
,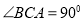 ,
,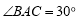 ,
,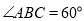 .
.操作发现:
(1)在如图1中,
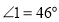 ,求
,求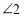 的度数;
的度数;(2)如图2,创新小组的同学把直线
 向上平移,并把
向上平移,并把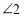 的位置改变,发现
的位置改变,发现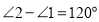 ,说明理由;
,说明理由;实践探究:
(3)缜密小组在创新小组发现结论的基础上,将如图中的图形继续变化得到如图,
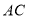 平分
平分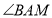 ,此时发现
,此时发现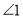 与
与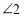 又存在新的数量关系,请直接写出
又存在新的数量关系,请直接写出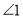 与
与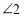 的数量关系.
的数量关系.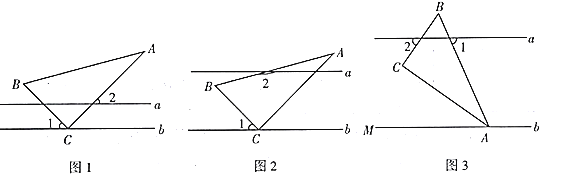
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两平行直线被第三条直线所截,则一对同旁内角的角平分线的关系是( )
A.互相垂直B.互相平行C.相交但不垂直D.以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2, 0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位长度秒匀速运动,物体乙按顺时针方向以2个单位长度秒匀速运动,则两个物体运动后的第2020次相遇点的坐标是( )

A.(2,0)B.(-1,-1)C.( -2,1)D.(-1, 1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于( )
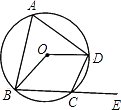
A.69°
B.42°
C.48°
D.38° -
科目: 来源: 题型:
查看答案和解析>>【题目】某校举办“红歌伴我成长”歌咏比赛活动,参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如图:
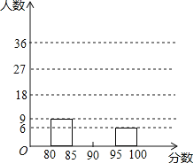
分数段
频数
频率
80≤x<85
9
0.15
85≤x<90
m
0.45
90≤x<95
■
■
95≤x<100
6
n
(1)求m,n的值分别是多少;
(2)请在图中补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段?
相关试题

