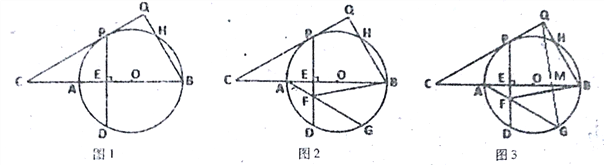
【题目】已知:如图,AB为⊙O的直径,C是BA延长线上一点,CP切⊙O于P,弦PD⊥AB于E,过点B作BQ⊥CP于Q,交⊙O于H.
(1)如图1,求证:PQ=PE;
(2)如图2,G是圆上一点,∠GAB=30![]() ,连接AG交PD于F,连接BF,tan∠BFE=
,连接AG交PD于F,连接BF,tan∠BFE=![]() ,求∠C的度数;
,求∠C的度数;
(3)如图3,在(2)的条件下,PD=6![]() ,连接QG交BC于点M,求QM的长.
,连接QG交BC于点M,求QM的长.
参考答案:
【答案】(1)证明见解析(2)30°(3) QM=![]()
【解析】试题分析:
(1)连接OP,PB,由已知易证∠OBP=∠OPB=∠QBP,从而可得BP平分∠OBQ,结合BQ⊥CP于点Q,PE⊥AB于点E即可由角平分线的性质得到PQ=PE;
(2)如下图2,连接OP,则由已知易得∠CPO=∠PEC=90°,由此可得∠C=∠OPE,设EF=x,则由∠GAB=30°,∠AEF=90°可得AE= ![]() ,在Rt△BEF中,由tan∠BFE=
,在Rt△BEF中,由tan∠BFE=![]() 可得BE=
可得BE= ![]() ,从而可得AB=
,从而可得AB= ![]() ,则OP=OA=
,则OP=OA= ![]() ,结合AE=
,结合AE= ![]() 可得OE=
可得OE= ![]() ,这样即可得到sin∠OPE=
,这样即可得到sin∠OPE=![]() ,由此可得∠OPE=30°,则∠C=30°;
,由此可得∠OPE=30°,则∠C=30°;
(3)如下图3,连接BG,过点O作OK⊥HB于点K,结合BQ⊥CP,∠OPQ=90°,可得四边形POKQ为矩形.由此可得QK=PO,OK∥CQ从而可得∠KOB=∠C=30°;由已知易证PE=![]() ,在Rt△EPO中结合(2)可解得PO=6,由此可得OB=QK=6;在Rt△KOB中可解得KB=3,由此可得QB=9;在△ABG中由已知条件可得BG=6,∠ABG=60°;过点G作GN⊥QB交QB的延长线于点N,由∠ABG=∠CBQ=60°,可得∠GBN=60°,从而可得解得GN=
,在Rt△EPO中结合(2)可解得PO=6,由此可得OB=QK=6;在Rt△KOB中可解得KB=3,由此可得QB=9;在△ABG中由已知条件可得BG=6,∠ABG=60°;过点G作GN⊥QB交QB的延长线于点N,由∠ABG=∠CBQ=60°,可得∠GBN=60°,从而可得解得GN=![]() ,BN=3,由此可得QN=12,则在Rt△BGN中可解得QG=
,BN=3,由此可得QN=12,则在Rt△BGN中可解得QG=![]() ,由∠ABG=∠CBQ=60°可知△BQG中BM是角平分线,由此可得QM:GM=QB:GB=9:6由此即可求得QM的长了.
,由∠ABG=∠CBQ=60°可知△BQG中BM是角平分线,由此可得QM:GM=QB:GB=9:6由此即可求得QM的长了.
试题解析:
(1)如下图1,连接OP,PB,∵CP切⊙O于P,
∴OP⊥CP于点P,
又∵BQ⊥CP于点Q,
∴OP∥BQ,
∴∠OPB=∠QBP,
∵OP=OB,
∴∠OPB=∠OBP,
∴∠QBP=∠OBP,
又∵PE⊥AB于点E,
∴PQ=PE;
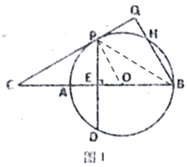
(2)如下图2,连接![]() ,∵CP切⊙O于P,
,∵CP切⊙O于P,
∴![]()
∴![]()
∵PD⊥AB
∴![]()
∴![]()
∴![]()
在Rt![]() 中,∠GAB=30°
中,∠GAB=30°
∴设EF=x,则![]()
在Rt![]() 中,tan∠BFE=3
中,tan∠BFE=3![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴在Rt![]() PEO中,
PEO中, ![]()
∴![]() 30°;
30°;
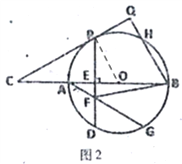
(3)如下图3,连接BG,过点O作![]() 于K,又BQ⊥CP,
于K,又BQ⊥CP,
∴![]() ,
,
∴四边形POKQ为矩形,
∴QK=PO,OK//CQ,
∴![]() 30°,
30°,
∵⊙O 中PD⊥AB于E ,PD=6![]() ,AB为⊙O的直径,
,AB为⊙O的直径,
∴PE= ![]() PD= 3
PD= 3![]() ,
,
根据(2)得![]() ,在Rt
,在Rt![]() EPO中,
EPO中, ![]() ,
,
∴![]() ,
,
∴OB=QK=PO=6,
∴在Rt![]() 中,
中, ![]() ,
,
∴![]() ,
,
∴QB=9,
在△ABG中,AB为⊙O的直径,
∴![]() AGB=90°,
AGB=90°,
∵![]() BAG=30°,
BAG=30°,
∴BG=6, ![]() ABG=60°,
ABG=60°,
过点G作GN⊥QB交QB的延长线于点N,则∠N=90°,∠GBN=180°-∠CBQ-∠ABG=60°,
∴BN=BQ·cos∠GBQ=3,GN=BQ·sin∠GBQ=![]() ,
,
∴QN=QB+BN=12,
∴在Rt△QGN中,QG=![]() ,
,
∵∠ABG=∠CBQ=60°,
∴BM是△BQG的角平分线,
∴QM:GM=QB:GB=9:6,
∴QM=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在正方形ABCD外取点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P,已知AE=AP=BE=1.
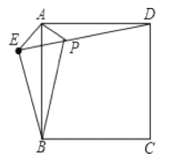
(1)求证:△APD≌△AEB;
(2)连接PC,求线段PC的长度;
(3)试求正方形ABCD的面积。
-
科目: 来源: 题型:
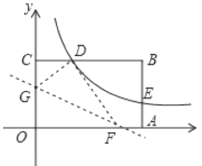
查看答案和解析>>【题目】如图,矩形OABC的顶点A. C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y=
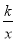 (k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,
(k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,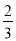 ).
).
(1)求反比例函数的表达式和m的值;
(2)将矩形OABC的进行折叠,使点O于点D重合,折痕分别与x轴、y轴正半轴交于点F,G,求折痕FG所在直线的函数关系式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AF平分∠BAE,CF平分∠DCE.
(1)如图①,已知AB∥CD,求证:∠AEC=∠C-∠A;
(2)如图②,在(1)的条件下,直接写出∠E与∠F的关系.
∠E= (用含有∠F的式子表示)
(3)如图③,BD⊥AB,垂足为B,∠BDC=110°,∠AEC=40°,求∠AFC的度数.
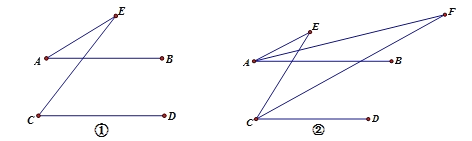
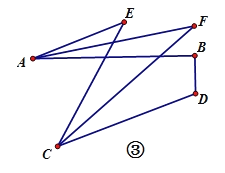
-
科目: 来源: 题型:
查看答案和解析>>【题目】为喜迎中华人民共和国成立70周年,博文中学将举行以“歌唱祖国”为主题的歌咏比赛,七年级需要在文具店购买国旗图案贴纸和小红旗发给学生做演出道具.已知每袋贴纸有50张,每袋小红旗有20面,贴纸和小红旗需整袋购买.两家文具店的标价相同,每袋贴纸价格比每袋小红旗价格少5元,而且4袋贴纸与3袋小红旗价格相同.
(1)求每袋国旗图案贴纸和每袋小红旗的价格各是多少元?
(2)如果购买贴纸和小红旗共90袋,给每位演出学生分发国旗图案贴纸2张,小红旗1面,恰好全部分完,请问该校七年级有多少名学生?
(3)在(2)条件下,两家文具店的有优惠如下:
A.文具店:全场商品购物超过800元后,超出800元的部分打八五折;
B.文具店:相同商品,“买十件赠一件”.
请问在哪家文具店购买比较优惠?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B两个蔬菜市场各有蔬菜14吨,现要全部运往甲、乙两地,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从蔬菜市场A到甲地运费50元/吨,到乙地30元/吨;从蔬菜市场B到甲地运费60元/吨,到乙地45元/吨。
(1)设从蔬菜市场A向甲地运送蔬菜x吨,请完成下表:
运往甲地(单位:吨)
运往乙地(单位:吨)
蔬菜市场A
x
蔬菜市场B
(2)若总运费为1300元,则从蔬菜市场A向甲地运送蔬菜多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点O为坐标原点,抛物线
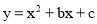 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),直线
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),直线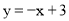 经过B、C两点.
经过B、C两点.(1)求抛物线的解析式;
(2)点P是x轴下方抛物线上一点,连接AC,过点P作PQ∥AC交BC于点Q,过点Q作x轴的平行线,过点P作y轴的平行线,两条直线相交于点K,PK交BC于点H,设QK的长为t,PH的长为d,求d与t之间的函数关系式;(不要求写出自变量t的取值范围)
(3)在(2)的条件下,PK交x轴于点R,过点R作RT⊥PQ,垂足为T,当PK=
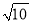 PT时,将线段QT绕点Q逆时针旋转90
PT时,将线段QT绕点Q逆时针旋转90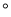 得到线段QL,M是线段PQ上一动点,过点M作直线AC的垂线,垂足为N,连接ON、ML,当ML∥ON时,求N点坐标.
得到线段QL,M是线段PQ上一动点,过点M作直线AC的垂线,垂足为N,连接ON、ML,当ML∥ON时,求N点坐标.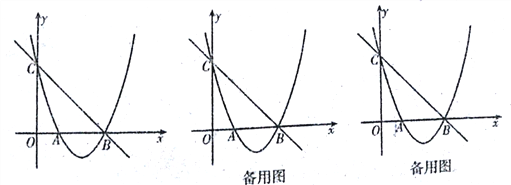
相关试题

