【题目】已知:如图,在正方形ABCD外取点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P,已知AE=AP=BE=1.
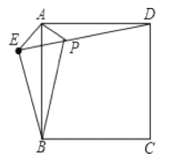
(1)求证:△APD≌△AEB;
(2)连接PC,求线段PC的长度;
(3)试求正方形ABCD的面积。
参考答案:
【答案】(1)见解析(2)![]() (3)2+
(3)2+![]()
【解析】
(1)由四边形ABCD是正方形,得到AB=AD,∠BAD=90°,由AE⊥AP,得到∠EAP=90°,于是得到∠EAB=∠DAP,即可得到结论;
(2)连接PB,PC,由(1)证得△APD≌△AEB,于是得到PD=AE,∠ADO=∠ABE,推出△ABP≌△DCP,得到PB=PC,根据勾股定理即可得到结论;
(3)过A作AM⊥PE于M,根据等腰直角三角形的性质得到AM=PM=![]() ,求出DM=1+
,求出DM=1+![]() ,由勾股定理得到AD=
,由勾股定理得到AD=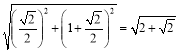 ,于是得到结果.
,于是得到结果.
(1)∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵AE⊥AP,
∴∠EAP=90°,
∴∠EAB=∠DAP,
在△APD与△AEB中,
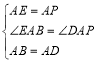 ,
,
∴△APD≌△AEB;
(2)连接PB,PC,由(1)证得△APD≌△AEB,
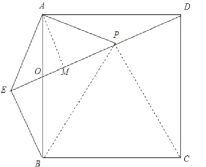
∴PD=AE,∠ADO=∠ABE,
∵AE=AP,
∴PD=AP,
∴∠PAD=∠PDA,
∴∠BAP=∠CDP,
在△ABP与△DCP中,
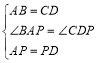 ,
,
∴△ABP≌△DCP,
∴PB=PC,
∵∠BOE=∠AOP,
∴∠BEO=∠BAD=90°,
∵PE=![]() AP=
AP=![]() ,
,
∴PB=![]() ,
,
∴PC=PB=![]() ;
;
(3)过A作AM⊥PE于M,
∴AM=PM=![]() PE=
PE=![]() ,
,
∴DM=1+![]() ,
,
∴AD=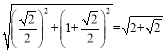 ,
,
∴正方形ABCD的面积=AD![]() =2+
=2+![]() .
.
-
科目: 来源: 题型:
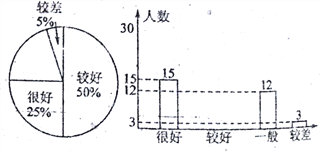
查看答案和解析>>【题目】我国北方又进入了交通事故频发的季节,为此,某校在全校2000名学生中随机抽取一部分人进行“交通安全”知识问卷调查活动,对问卷调查成绩按“很好”、“较好”、“一般”、“较差”四类汇总分析,并绘制了如下扇形统计图和条形统计图.
(1)本次活动共抽取了多少名同学?
(2)补全条形统计图;
(3)根据以上调查结果分析,估计该校2000名学生中,对“交通安全”知识了解一般的学生约有多少名?
-
科目: 来源: 题型:
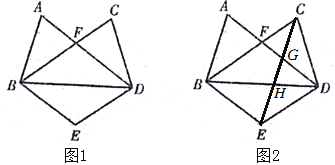
查看答案和解析>>【题目】如图,AD与BC相交于点F,FA=FC,∠A=∠C,点E在BD的垂直平分线上.
(1)如图1,求证:∠FBE=∠FDE;
(2)如图2,连接CE分别交BD、AD于点H、G,当∠FBD=∠DBE=∠ABF,CD=DE时,直接写出所有与△ABF全等的三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】服装店老板用4500元购进一批某款T恤衫,由于深受顾客喜爱,很快售完,老板又用4950元购进第二批该款式T恤衫,所购数量与第一批相同,但每件进价比第一批多了9元.
(1)第一批该款式T恤衫每件进价是多少元?
(2)老板以每件120元的价格销售该款式T恤衫,当第二批T恤衫售出
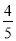 时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价-进价)
时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价-进价) -
科目: 来源: 题型:
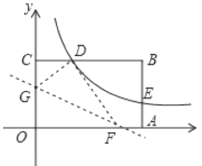
查看答案和解析>>【题目】如图,矩形OABC的顶点A. C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y=
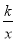 (k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,
(k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3,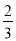 ).
).
(1)求反比例函数的表达式和m的值;
(2)将矩形OABC的进行折叠,使点O于点D重合,折痕分别与x轴、y轴正半轴交于点F,G,求折痕FG所在直线的函数关系式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AF平分∠BAE,CF平分∠DCE.
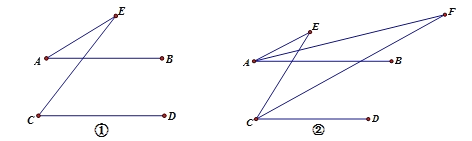
(1)如图①,已知AB∥CD,求证:∠AEC=∠C-∠A;
(2)如图②,在(1)的条件下,直接写出∠E与∠F的关系.
∠E= (用含有∠F的式子表示)
(3)如图③,BD⊥AB,垂足为B,∠BDC=110°,∠AEC=40°,求∠AFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB为⊙O的直径,C是BA延长线上一点,CP切⊙O于P,弦PD⊥AB于E,过点B作BQ⊥CP于Q,交⊙O于H.
(1)如图1,求证:PQ=PE;
(2)如图2,G是圆上一点,∠GAB=30
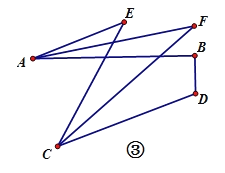
 ,连接AG交PD于F,连接BF,tan∠BFE=
,连接AG交PD于F,连接BF,tan∠BFE=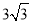 ,求∠C的度数;
,求∠C的度数;(3)如图3,在(2)的条件下,PD=6
 ,连接QG交BC于点M,求QM的长.
,连接QG交BC于点M,求QM的长.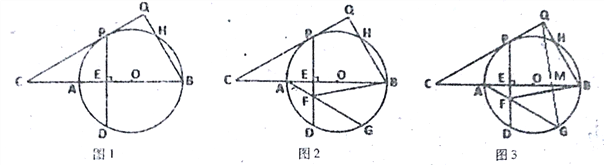
相关试题

