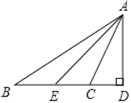
【题目】如图,在△ABC中,∠B=24°,∠ACB=104°,AD⊥BC交BC的延长线于点D,AE平分∠BAC.
(1)求∠DAE的度数.
(2)若∠B=α,∠ACB=β,其它条件不变,请直接写出∠DAE与α、β的数量关系.
参考答案:
【答案】(1)40°.(2)![]()
【解析】
(1)先根据三角形内角和定理求出∠BAC的度数,再根据角平分线的定义求出∠EAC的度数,由∠DAE=∠EAC+∠CAD即可得出结论.(2)与(1)同理可得∠DAE=![]() (β﹣α).
(β﹣α).
解:(1)∵在△ABC中,∠B=24°,∠ACB=104°,
∴∠BAC=180°﹣24°﹣104°=52°.
∵AE平分∠BAC,
∴∠BAE=![]() ∠BAC=26°,
∠BAC=26°,
∴∠AEC=∠B+∠BAC=24°+26°=50°.
∵AD⊥BC,
∴∠D=90°,
∴∠DAE=90°﹣∠AED=90°﹣50°=40°.
(2)∵AD⊥BC,
∴∠D=90°,
∴∠AED=90°﹣∠DAE,
在△ABE中,∠BAE=∠AED﹣∠B,
在△ACD中,∠ACB=∠CAD+∠D=∠DAE﹣∠CAE+90°,
∴∠CAE=∠DAE+90°﹣∠ACB,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∴90°﹣∠DAE﹣∠B=∠DAE+90°﹣∠ACB,
∴∠ACB=∠B+2∠DAE,即∠DAE=![]() (∠ACB﹣∠B),
(∠ACB﹣∠B),
∴∠DAE=![]() (β﹣α).
(β﹣α).
-
科目: 来源: 题型:
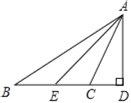
查看答案和解析>>【题目】如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )

A.4,30° B.2,60° C.1,30° D.3,60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组.
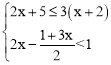 把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解.
把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
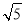 .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为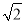 ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+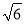 ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+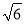 .其中正确结论的序号是( )
.其中正确结论的序号是( )
A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, 于
于 ,
, ,且
,且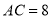 ,则
,则 的长度是( )
的长度是( )
A.3B.4C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax+bx+c(a≠0)的图像如图所示,则下列结论中正确的是( )

A.a>0 B.3是方程ax+bx+c=0的一个根
C.a+b+c=0 D.当x<1时,y随x的增大而减小
-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
相关试题

