【题目】观察下列两个等式:3+2=3×2﹣1,4+![]() =4×
=4×![]() ﹣1,给出定义如下:
﹣1,给出定义如下:
我们称使等式a+b=ab﹣1成立的一对有理数a,b为“椒江有理数对”,记为(a,b),如:数对(3,2),(4,![]() )都是“椒江有理数对”.
)都是“椒江有理数对”.
(1)数对(﹣2,1),(5,![]() )中是“椒江有理数对”的是 ;
)中是“椒江有理数对”的是 ;
(2)若(a,3)是“椒江有理数对”,求a的值;
(3)若(m,n)是“椒江有理数对”,则(﹣n,﹣m) “椒江有理数对”(填“是”、“不是”或“不确定”).
(4)请再写出一对符合条件的“椒江有理数对”
(注意:不能与题目中已有的“椒江有理数对”重复)
参考答案:
【答案】(1)(﹣2,1)不是“椒江有理数对”, (5,![]() )中是“椒江有理数对”(2)2(3)不是;(4)(6,1.4).
)中是“椒江有理数对”(2)2(3)不是;(4)(6,1.4).
【解析】
(1)根据“椒江有理数对”的定义即可判断;
(2)根据“椒江有理数对”的定义,构建方程即可解决问题;
(3)根据“椒江有理数对”的定义即可判断;
(4)根据“椒江有理数对”的定义即可解决问题.
(1)![]()
∴![]()
∴![]() 不是“椒江有理数对”,
不是“椒江有理数对”,
∵![]()
∴![]()
∴![]() 是“椒江有理数对”;
是“椒江有理数对”;
(2)由题意得:
![]()
解得![]()
(3)不是.
理由:![]()
![]() ,
,
∵![]() 是“椒江有理数对”
是“椒江有理数对”
∴![]()
∴![]()
∴![]() 不是“椒江有理数对”,
不是“椒江有理数对”,
(4)![]() 等.
等.
故答案为:![]() ;不是;
;不是;![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC.
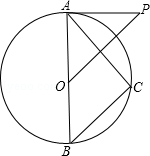
(1)求证:PA为⊙O的切线;
(2)若OB=5,OP=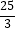 ,求AC的长.
,求AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC上.若BE=3,EC=5,则AB的长为_____.
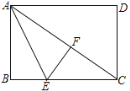
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.

(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,
①当∠EAC=90°时,求PB的长;
②直接写出旋转过程中线段PB长的最小值与最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系,A(-2,0),B(0,3),点M在直线y=
 x 上,且SΔMAB=6,则点M的坐标为_____.
x 上,且SΔMAB=6,则点M的坐标为_____.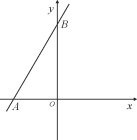
-
科目: 来源: 题型:
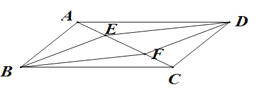
查看答案和解析>>【题目】如图,□ABCD,BE//DF,且分别交对角线AC于点E,F,连接ED,BF .
求证:(1)ΔABE≌ΔCDF;
(2)∠DEF=∠BFE.
相关试题

