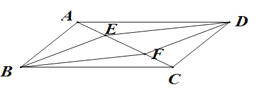
【题目】如图,□ABCD,BE//DF,且分别交对角线AC于点E,F,连接ED,BF .
求证:(1)ΔABE≌ΔCDF;
(2)∠DEF=∠BFE.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)首先由平行四边形的性质可得AB=CD,AB∥CD,再根据平行线的性质可得∠BAE=∠DCF,∠BEC=∠DFA,即可根据AAS定理判定△ABE≌△CDF;
(2)只要证明四边形BEDF是平行四边形,推出DE∥BF即可证明.
证明:(1)在□ABCD中,
AB=CD,AB∥CD,
∴∠BAC=∠DCA,
又∵BE∥DF,
∴∠BEF=∠DFE,
∴∠AEB=∠CFD,
在△ABE和△CDF中,
∵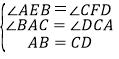 ,
,
∴ΔABE≌ΔCDF(AAS);
(2)由(1)知,BE=DF,
又∵BE∥DF,
∴四边形BEDF是平行四边形,
∴DE∥BF,
∴∠DEF=∠BFE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列两个等式:3+2=3×2﹣1,4+
 =4×
=4× ﹣1,给出定义如下:
﹣1,给出定义如下:我们称使等式a+b=ab﹣1成立的一对有理数a,b为“椒江有理数对”,记为(a,b),如:数对(3,2),(4,
 )都是“椒江有理数对”.
)都是“椒江有理数对”.(1)数对(﹣2,1),(5,
 )中是“椒江有理数对”的是 ;
)中是“椒江有理数对”的是 ;(2)若(a,3)是“椒江有理数对”,求a的值;
(3)若(m,n)是“椒江有理数对”,则(﹣n,﹣m) “椒江有理数对”(填“是”、“不是”或“不确定”).
(4)请再写出一对符合条件的“椒江有理数对”
(注意:不能与题目中已有的“椒江有理数对”重复)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.

(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,
①当∠EAC=90°时,求PB的长;
②直接写出旋转过程中线段PB长的最小值与最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系,A(-2,0),B(0,3),点M在直线y=
 x 上,且SΔMAB=6,则点M的坐标为_____.
x 上,且SΔMAB=6,则点M的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两直线l1 , l2分别经过点A(1,0),点B(﹣3,0),并且当两直线同时相交于y正半轴的点C时,恰好有l1⊥l2 , 经过点A、B、C的抛物线的对称轴与直线l1交于点K,如图所示.
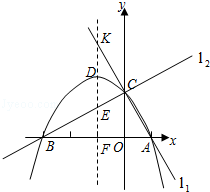
(1)求点C的坐标,并求出抛物线的函数解析式;
(2)抛物线的对称轴被直线l1 , 抛物线,直线l2和x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由;
(3)当直线l2绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】“幸福是奋斗出来的”,在数轴上,若C到A的距离刚好是3,则C点叫做A的“幸福点”,若C到A、B的距离之和为6,则C叫做A、B的“幸福中心”
(1)如图1,点A表示的数为﹣1,则A的幸福点C所表示的数应该是 ;
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2,点C就是M、N的幸福中心,则C所表示的数可以是 (填一个即可);
(3)如图3,A、B、P为数轴上三点,点A所表示的数为﹣1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以2个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的幸福中心?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD中折叠,使顶点B落在边AD的E点上折痕FG交BC于G,交AB于F,若∠AEF=20°,则∠FGB的度数为( )
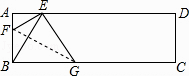
A.25°
B.30°
C.35°
D.40°
相关试题

