【题目】某校八年级学生数学科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的,如果期末评价成绩80分以上(含80分),则评为“优秀”.下面表中是小张和小王两位同学的成绩记录:
完成作业 | 单元检测 | 期末考试 | |
小张 | 70 | 90 | 80 |
小王 | 60 | 75 |
(1)若按三项成绩的平均分记为期末评价成绩,请计算小张的期末评价成绩;
(2)若按完成作业、单元检测、期末考试三项成绩按1:2:m的权重,小张的期末评价成绩为81分,则小王在期末(期末成绩为整数)应该最少考多少分才能达到优秀?
参考答案:
【答案】(1)80分;(2)小王在期末应该至少考85分才能达到优秀.
【解析】分析:(1)小张期末评价成绩=(小张完成作业分+小张的单元检测+小张期末考试分)÷3,
(2)先根据小张期末评价成绩及小张三项成绩求出期末考试成绩的权重.因为期末评价成绩至少80分才是优秀,所以根据题意依据小王的期末评价成绩80分来计算他的期末考试成绩即可.
详解:(1)小张的期末评价成绩=![]() =80,
=80,
答:小张的期末评价成绩是80分;
(2)依题意得,70×![]() +90×
+90×![]() +80×
+80×![]() =81
=81
解得:m=7,
经检查,m=7是所列方程的解.
设小王期末考试分数为x,依题意列方程得
60×![]() +75×
+75×![]() +
+![]() x=80,
x=80,
解得:x=84![]() ≈85,
≈85,
答:小王在期末应该至少考85分才能达到优秀.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了锻炼学生身体素质,训练定向越野技能,某校在一公园内举行定向越野挑战赛.路线图如图
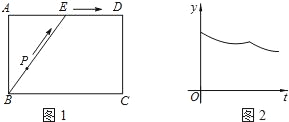 所示,点
所示,点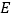 为矩形
为矩形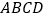 边
边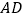 的中点,在矩形
的中点,在矩形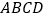 的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员
的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员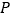 从点
从点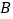 出发,沿着
出发,沿着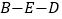 的路线匀速行进,到达点
的路线匀速行进,到达点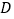 .设运动员
.设运动员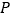 的运动时间为
的运动时间为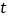 ,到监测点的距离为
,到监测点的距离为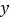 .现有
.现有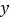 与
与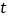 的函数关系的图象大致如图
的函数关系的图象大致如图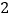 所示,则这一信息的来源是( ).
所示,则这一信息的来源是( ).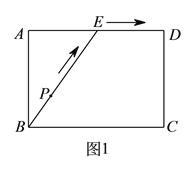

A. 监测点
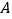 B. 监测点
B. 监测点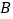 C. 监测点
C. 监测点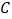 D. 监测点
D. 监测点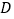
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=6cm,AC=8cm,BC=10cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E,线段DE的最小值是 cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形,AC、DE相交于点O.
(1)求证:四边形ADCE是矩形.
(2)若∠AOE=60°,AE=4,求矩形ADCE对角线的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)
 ″
″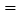 ________;(2)
________;(2)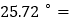 _______°________
_______°________ ________″;
________″;(3)
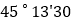 ″
″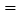 ________
________ .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,等腰三角形ABO的底边OA在x轴上,顶点B在反比例函数y=
 (x>0)的图象上,当底边OA上的点A在x轴的正半轴上自左向右移动时,顶点B也随之在反比例函数y=
(x>0)的图象上,当底边OA上的点A在x轴的正半轴上自左向右移动时,顶点B也随之在反比例函数y=  (x>0)的图象上滑动,但点O始终位于原点.
(x>0)的图象上滑动,但点O始终位于原点.
(1)如图①,若点A的坐标为(6,0),求点B的坐标;
(2)当点A移动到什么位置时,三角形ABO变成等腰直角三角形,请说明理由;
(3)在(2)中,如图②,△PA1A是等腰直角三角形,点P在反比例函数y= (x>0)的图象上,斜边A1A在x轴上,求点A1的坐标.
(x>0)的图象上,斜边A1A在x轴上,求点A1的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF,∠ECA=∠FCA.
(1)求证:四边形AFCE是菱形;
(2)若AB=8,BC=4,求菱形AFCE的面积.

相关试题

